Решение уравнений и неравенств
Решение уравнений в целочисленном виде – isolve
Иногда бывает нужен результат в форме только целых чисел. Для этого используется функция isolve(eqns, vans), дающая решение в виде целых чисел. Приведем примеры ее применения:
> isolve({2*x-5=3*y}):
{x = 4 + 3_Zl,y=\ + 2_Z1]
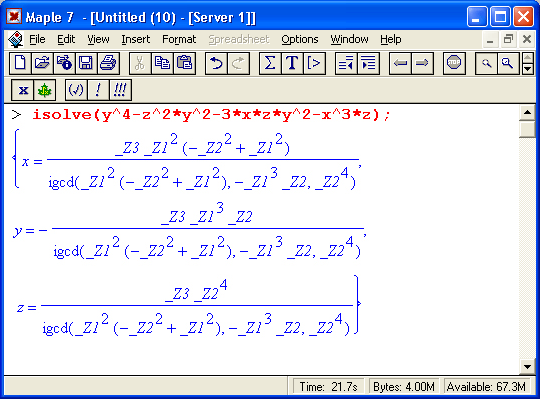
> isolve(y^4-z^2*y^2-3*x*z*y*2-x^3*z);
Во втором из приведенных примеров в выводе появилась вспомогательная переменная %1, которая упрощает запись результата при текстовом формате его вывода (Character Notation). Напоминаем, что в стандартной математической нотации вспомогательная переменная вида %N не формируется. В этом случае упомянутый пример будет выглядеть следующим образом:
Результат вычислений одинаков при любом формате вывода, но иногда вывод в текстовом формате с выделением вспомогательных переменных имеет преимущество, поскольку выглядит более компактным.
Функция msolve
Функция msolve(eqns,vars.m) или msolve(eqns,m) обеспечивает решение вида Z mod m (то есть при подстановке решения левая часть 4 при делении на т дает остаток, равный правой части уравнения). При отсутствии решения возвращается объект NULL (пустой список).
Ниже даны примеры использования функции msolve:
> msolve({3*x-4*y=1, 7*x+y=2}.12);
{у = 5,х=3}
> msolve(2^i=3.19);
{(=13 + 18_Z7~}
> msolve(8*j-2,x,17);
{/ = 3 + 8*}
На этом мы завершаем рассмотрение функций для решения уравнений, неравенств и систем с ними.
Что нового мы узнали?
В этом уроке мы научились:
- Вычислять суммы членов последовательностей.
- Вычислять произведения членов последовательностей.
- Вычислять производные.
- Вычислять интегралы.
- Разлагать функции в ряды.
- Решать уравнения и неравенства.
