Решение уравнений и неравенств
Решение рекуррентных уравнений – rsolve
Функция solve имеет ряд родственных функций. Одну из таких функций – fsolve – мы рассмотрели выше. В справочной системе Maple 7 можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т. д. Здесь мы рассмотрим решение уравнений важного класса – рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.
Для решения рекуррентных уравнений используется функция rsolve:
rsolve(eqns, fens), rsolve(eqris .fens, 'genfunc'(z)) rsolve(eqns, fens, 'makeproc')
Здесь eqns – одиночное уравнение или система уравнений, fens – функция, имя функции или множество имен функций, z – имя, генерирующее функциональную переменную.
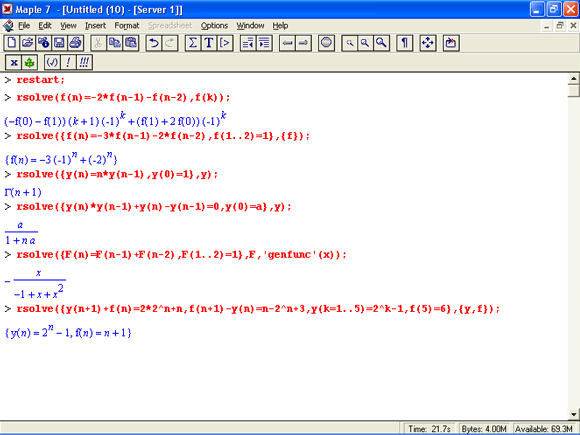
Ниже представлены примеры применения функции rsolve:
А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением:
> eql: -(f(n+2) = f(rn-l) + f(n) .f(0) -1 .f(l) -1}:
eql~{f(n+2) = f(n + \) + f(n),f(0)=\,f(l)=l}
В нем задана рекуррентная формула для числа Фибоначчи – каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve можно получить поистине ошеломляющий результат:
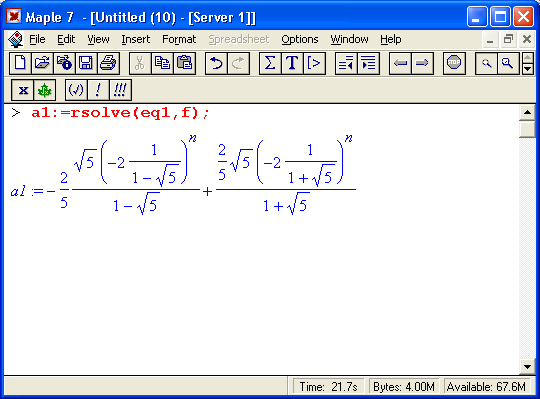
Числа Фибоначчи – целые числа. Поэтому представленный результат выглядит как весьма сомнительный. Но на самом деле он точный и с его помощью можно получить числа Фибоначчи. Ниже показан процесс получения чисел Фибоначчи для n = 5, 7, 10 и 20:
> [normal(subs(n=5,al).expanded).normal(subs(n-7.al).expanded). normal(subs(n=10,al),expanded),normal(subs(n=20.al),expanded)]; [8.21.89.10946]
