Операции с полиномами
Определение полиномов
К числу наиболее известных и изученных аналитических функций относятся степенные многочлены – полиномы. Графики полиномов описывают огромное разнообразие кривых на плоскости. Кроме того, возможны рациональные полиномиальные выражения в виде отношения полиномов. Таким образом, круг объектов, которые могут быть представлены полиномами, достаточно обширен, и полиномиальные преобразования широко используются на практике, в частности, для приближенного представления других функций.
Под полиномом в системе Maple 7 понимается сумма выражений с целыми степенями. Многочлен для ряда переменных – многомерный полином. К одномерным полиномам относятся степенной многочлен:
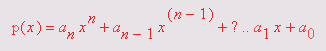
А также отдельная переменная х и константа. Большое достоинство полиномов состоит в том, что они дают единообразное представление многих зависимостей и для своего вычисления требуют только арифметических операций (их число значительно сокращается при использовании хорошо известной схемы Горнера). Производные от полиномов и интегралы с подынтегральными функциями-полиномами легко вычисляются и имеют простой вид. Есть и достаточно простые алгоритмы для вычисления всех (в том числе комплексных) корней полиномов на заданном промежутке.
Выделение коэффициентов полиномов
Для выделения коэффициентов полиномов в Maple 7 служат следующие функции:
- coeff(p, х) – возвращает коэффициент при х полинома р;
- coeff(p.x.n) – возвращает коэффициент для члена со степенью n полинома р;
- coeff(p.x^n) – возвращает коэффициенты при х^n полинома р;
- coeffs(p, х, 't') – возвращает коэффициенты полинома нескольких переменных, относящиеся к переменной х (или списку переменных) с опцией ' t', задающей имя переменной;
- collect(p,x) – возвращает полином, объединяя коэффициенты при степенях переменной х.
Ниже даны примеры применения этих функций:
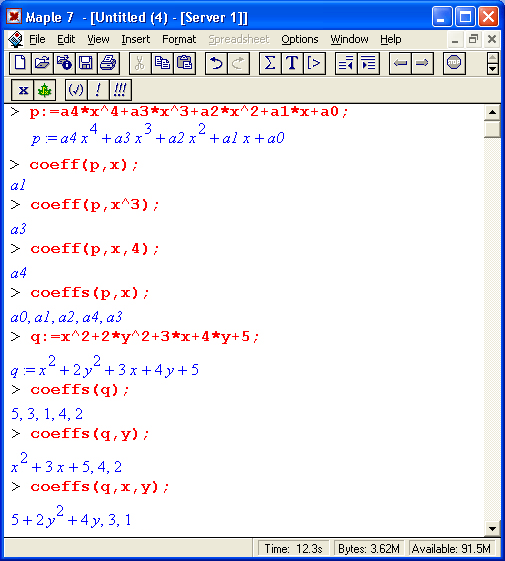
Примечание
Следует обратить внимание на то, что при выполнении операции collect в прежних версиях Maple довольно часто возникала фатальная ошибка. Как видно из приведенных примеров, в Maple 7 такой ошибки уже не возникает.
