Занимательные фигуры – трехмерные графики
Параметрическое задание уравнений поверхности открывает почти неисчерпаемые возможности построения занимательных и сложных фигур самого различного вида. Приведем пару построений такого рода.
На рис. 11.24 показан тор, сечение которого имеет вид сплюснутой шестиконечной звезды. Вырез в фигуре дает прекрасный обзор ее внутренней поверхности, а цветная функциональная окраска и линии сетки, построенные с применением алгоритма удаления невидимых линий, дают весьма реалистичный вид фигуры.
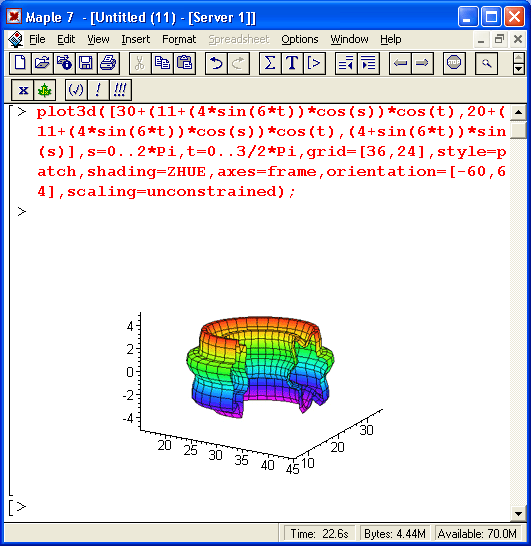
Рис. 11.24. Тор с сечением в виде шестиконечной звезды
Замените параметр scaling=unconstrained на scaling=constrained, и вы получите тор с неискаженным сечением.
На рис. 11.25 показан еще один тор. На этот раз он круглого сечения, но сверху и снизу имеет вид пятиконечной звезды.
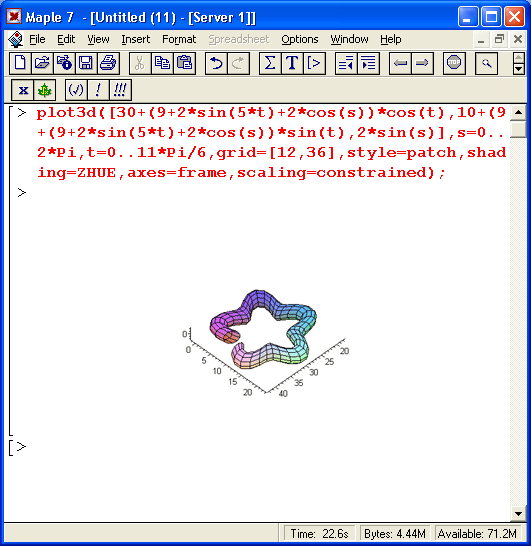
Рис. 11.25. Тор круглого сечения в виде пятиконечной звезды
Примечание
В приведенных на рис. 11.19-11.25 программах построения различных поверхностей и трехмерных фигур имеется ряд характерных констант и математических выражений, определяющих как вид фигур, так и их размеры и положение. Рекомендуется тщательно проанализировать эти примеры и попробовать их в работе с несколько измененными теми или иными данными. Полезно построить ряд подобных примеров самостоятельно. Все это будет способствовать привитию учащимся специального геометрического стиля мышления, при котором геометрические особенности фигур связываются с их расчетным описанием.
