Системы координат
В этот раздел мы вставили страницу из старого учебника по планиметрии и расширили ее до третьего измерения.
В двумерном пространстве две пересекающиеся линии определяют поверхность плоскости. Чтобы определить положение в пространстве, вы должны знать только расстояние каждой линии до точки их пересечения.
Чтобы определить трехмерное пространство, вам нужно добавить третью линию, лежащую в другой плоскости. Для определения положения в трехмерном пространстве вы должны измерить расстояние до трех линий, а не до двух.
В планиметрии прямые, определяющие пространство, называются осями X и Y (X and Y axes). Точка, в которой они пересекаются, является началом координат (origin). Точка пересечения имеет координаты (0.0) – см. рис. 3.2.
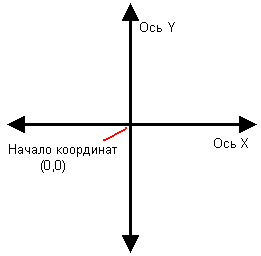
Рис. 3.2. Прямоугольные (декартовы) координаты
В трехмерной геометрии третья линия называется Z, и она пересекается с двумя другими линиями в начале координат.
В трехмерном пространстве точка пересечения имеет координаты (0, 0, 0) – рис. 3.3.
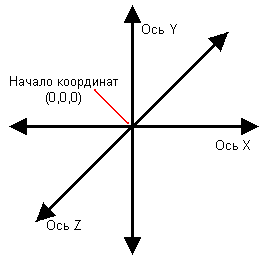
Рис. 3.3. Добавив ось Z к прямоугольным координатам, можно измерить глубину
Когда оси X, Y и Z имеют фиксированное положение и ориентацию в пространстве, они определяют абсолютную (неподвижную) систему координат, которая называется глобальной системой координат (world coordinate system). Эта система отслеживает все объекты в пространстве относительно глобальных осей (рис. 3.4).
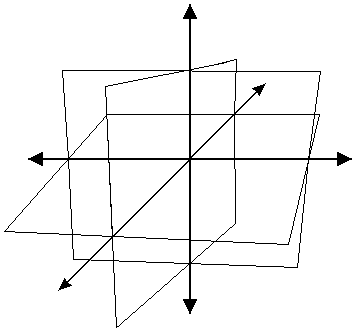
Рис. 3.4. Глобальная система координат используется для определения положения объекта в глобальном пространстве
Если оси не зафиксированы в пространстве, а привязаны к объектам, они определяют локальную систему координат (local coordinate system). Эта относительная система координат отслеживает изменение положения, ориентацию и масштаб объектов относительно их локальных осей (рис. 3.5).
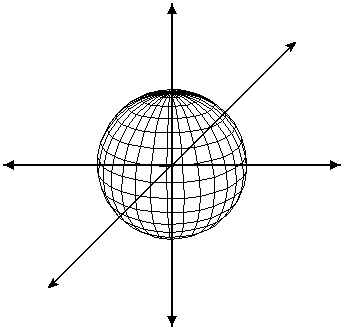
Рис. 3.5. Локальная система координат использует относительную систему координат для определения пространства объекта
