Сравнение более чем двух зависимых выборок
На основе данных по гипертонии исследуем, значимо ли изменяется содержание холестерина в течение четырех промежутков времени (такое сравнение для первых двух промежутков времени мы уже провели в параграфе 13.2).
Для достижения этой цели подходит однофакторный дисперсионный анализ с повторными измерениями. Пользователи SPSS, работавшие с этим пакетом на больших компьютерах, знают, что выполнить эту весьма распространенную операцию можно было только с помощью процедуры MANOVA (многомерный дисперсионный анализ). Ясно, что эта процедура предназначена для разнообразных методов многомерного анализа, но может быть использована при одномерном дисперсионном анализе с повторными измерениями.
Начиная с версии 7 SPSS процедура MANOVA была заменена процедурой GLM (General Linear Model). Однако и в текущей версии процедура MANOVA по прежнему остается доступной при использовании программного синтаксиса.
Разнообразные возможности анализа, предоставляемые этими процедурами (GLM и MANOVA), обеспечиваются ценой уже практически необозримого количества команд, спецификаций, параметров и ключевых слов. Даже при решении такой простой задачи, как рассматриваемая, надо уметь ориентироваться в этом многообразии. Несколько подробнее процедура GLM рассматривается в главе 17; однако в рамках этой книги невозможно охватить всю широту диапазона возможностей, предоставляемых этой процедурой. Теперь перейдем к решению нашей задачи при помощи однофакторного дисперсионного анализа с повторными измерениями.
- Загрузите файл hyper, sav.
- Выберите в меню команды Analyze (Анализ) › General Linear Model (Общая линейная модель) › Repeated Measures… (Повторные измерения)
Откроется диалоговое окно Repeated Measures Define Factor(s) (Определить фактор(ы) для повторных измерений).
В данном примере мы подвергнем анализу четыре переменных: cho10, cho11, cho16 и chol12; следовательно, фактор повторных измерений будет задаваться четырьмя уровнями (слоями).
- Введите число 4 в поле Number of Levels (Количество уровней). По умолчанию принимается имя фактора faktor1; при желании можно задать для него любое другое i имя (например, "время").
- Щелкните на кнопке Add. Других факторов повторных измерений у нас нет, поэтому можно сразу закрыть этот диалог кнопкой Define (Определить). Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 13.7).
- Перенесите переменные cho10, cho 11, cho16 и chol12 в список Within-Subject Variables (Переменные внутри субъекта); далее кнопками, которые находятся внизу диалогового окна, можно установить дополнительные параметры но мы не будем их рассматривать.
- Запустите вычисления, щелкнув на ОК.
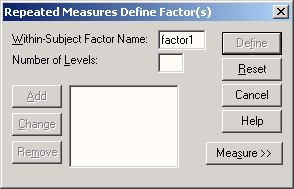
Рис. 13.6: Диалоговое окно Repeated Measures Define Factor(s)
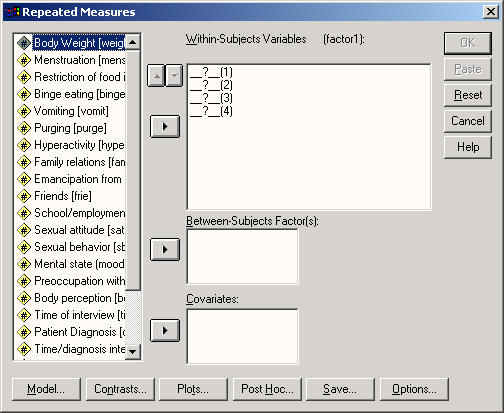
Рис. 13.7: Диалоговое окно Repeated Measures
- Проанализируйте результаты, появившиеся в окне просмотра.
Вы убедитесь, что для неподготовленного пользователя толкование полученных результатов расчета может составить большие трудности. Подробнее о них мы поговорим в главе 17. Теперь же мы ограничимся указанием, что результаты обычного дисперсионного анализа содержатся в строке "Sphericity assumed" (Предположение о сферичности) таблицы вывода, приведенной ниже:
Tests of Within-Subjects Effects (Тест эффектов внутри субъекта)
| Measure: MEASURE_1 | ||||||
| Source (Источник) | Type III Sum of Squares (Сумма квадратов типа III) | df | Mean Square (Среднее квадратов) | F | Sig. (Значимость) | |
| FACTOR1 | Sphericity Assumed (Принимается гипотеза о сферичности) | 3381.822 | 3 | 1127.274 | 2.653 | 0.048 |
| Greenhouse – Geisser | 3381.822 | 2.509 | 1347.779 | 2.653 | 0.058 | |
| Huynh-Feldt | 3381.822 | 2.549 | 1326.675 | 2.653 | 0.058 | |
| Lower Bound | 3381.822 | 1.000 | 3381.822 | 2.653 | 0.105 | |
| Error (FACTOR1) | Sphericity Assumed (Принимается гипотеза о сферичности) | 220504.678 | 519 | 424.865 | ||
| Greenhouse – Geisser | 220504.678 | 434.088 | 507.972 | |||
| Huynh-Feldt | 220504.678 | 440.994 | 500.018 | |||
| Lower Bound | 220504.678 | 173.000 | 1274.594 | |||
Вероятность ошибки р составляет 0.048, что указывает на значимое различие между отдельными моментами времени. К сожалению, даже в 10-й версии SPSS отсутствует возможность провести апостериорный тест для повторных измерений, чтобы выяснить, какие именно промежутки времени значимо отличаются друг от друга. В случае, если выявлены значимые отличия, как в рассмотренном примере, пользователю не остается ничего другого, кроме выполнения парного t-теста.