Явная схема Эйлера
Рассмотрим сначала математические аспекты построения разностной схемы для уравнения диффузии тепла, а затем приведем примеры работы разработанного алгоритма применительно к линейному и нелинейному уравнениям.
Построение разностной схемы
Используем для решения уравнения теплопроводности шаблон, изображенный на рис. 13.6. Для дискретизации второй производной по пространственной координате необходимо использовать три последовательных узла, в то время как для разностной записи первой производной по времени достаточно двух узлов. Записывая на основании данного шаблона дискретное представление для (i,k)-го узла, получим разностное уравнение.
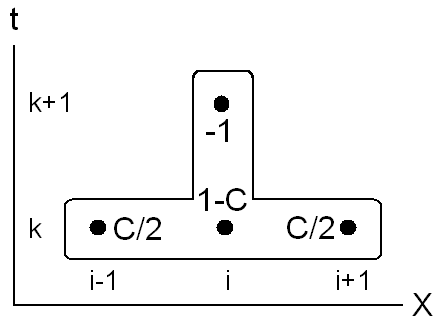
Рис. 13.6. Шаблон аппроксимации явной схемы для уравнения теплопроводности
Приведем в разностной схеме (8) подобные слагаемые, перенеся в правую часть значения сеточной функции с индексом k (как часто говорят, с предыдущего слоя по времени), а в левую – с индексом k-t-i (т. е. со следующего временного слоя). Кроме этого, введем коэффициент с, который будет характеризовать отношение шагов разностной схемы по времени и пространству Несколько забегая вперед, заметим, что значение параметра с, называемого коэффициентом Куранта, имеет большое значение для анализа устойчивости разностной схемы. С учетом этих замечаний, разностная схема (8) запишется в другом виде.
Множители для каждого из значений сеточной функции в узлах шаблона, соответствующие разностному уравнению (9), приведены рядом с каждой точкой шаблона на рис. 13.6. Фактически, геометрия шаблона и эти множители задают построенную нами разностную схему.
Несложно убедиться в том, что для получения замкнутой системы разностных алгебраических уравнений систему (9) необходимо дополнить дискретным представлением начального и граничных условий (6) и (7). Тогда число неизвестных будет в точности равно числу уравнений, и процесс формирования разностной схемы будет окончательно завершен.
Важно подчеркнуть, что возможная нелинейность полученной системы алгебраических уравнений определяется зависимостями от температуры функций D(u) и ф(и), т. е. как коэффициент диффузии, так и источник тепла могут быть функциями сеточной функции uik.
Если присмотреться к разностным уравнениям (9) повнимательнее, то можно сразу предложить несложный алгоритм реализации этой разностной схемы. Действительно, каждое неизвестное значение сеточной функции со следующего временного слоя, т. е. левая часть соотношения (9) явно выражается через три ее значения с предыдущего слоя (правая часть), которые уже известны. Таким образом, в случае уравнения теплопроводности нам очень повезло – для расчета 1-го слоя по времени следует попросту подставить в (9) начальное условие (известные значения и с нулевого слоя в узлах сетки), для расчета 2-го слоя достаточно использовать вычисленный таким образом набор и с 1-го слоя и т. д. Из-за того, что разностная схема сводится к такой явной подстановке, ее и называют явной, а благодаря пересчету значений с текущего слоя через ранее вычисленные слои – схемой бегущего счета.
