Неявная схема Эйлера
Алгоритм прогонки
Приведем в данном разделе описание чрезвычайно популярного алгоритма реализации неявных разностных схем, который называется методом прогонки. Этот алгоритм имел историческое значение для становления технологий расчетов уравнений в частных производных, и мы просто не можем не упомянуть о нем в этой книге.
Сразу оговоримся, что его применение для решения уравнений в частных производных в среде Mathcad может быть оправдано, только если Вы работаете с очень частыми сетками, которые приводят к системам разностных уравнений большой размерности и, соответственно, очень долгому времени вычислений.
Основным вычислительным ядром программы, реализующей на Mathcad неявную разностную схему, было решение (на каждом временном слое) системы линейных алгебраических уравнений, задаваемых матрицей А. Заметим, что эта матрица, как говорят, имеет диагональное преобладание, а точнее, является трехдиагональной (рис. 13.13). Все ее элементы, кроме элементов на главной диагонали и двух соседних диагоналях, равны нулю. С точки зрения оптимизации быстродействия алгоритма, применение встроенной функции isolve является весьма расточительным, поскольку основной объем арифметических операций, выполняемых компьютером (а он составляет, как нетрудно убедиться величину порядка M2), сводится к непроизводительному перемножению нулей.
Для отыскания решения линейных систем алгебраических уравнений имеется чрезвычайно эффективный алгоритм, называемый прогонкой, который позволяет снизить число арифметических операций на целый порядок, т. е. до значения порядка м. Это означает, что при использовании пространственных сеток с 1000 узлами выигрыш во времени вычислений составит величину порядка 103! Реализация данного алгоритма приведена в листинге 13.3, который является продолжением листинга 13.2, используя определенные в нем коэффициенты матрицы А, а также начальное условие.
Листинг 13.3. Алгоритм прогонки (продолжена листинга 13.2):
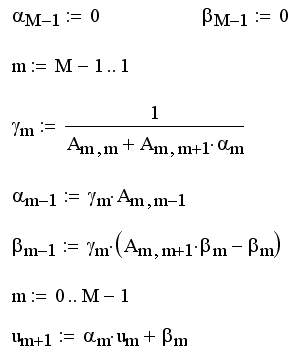
Программа листинга 13.3 осуществляет пересчет одного шага по времени, т. е. заменяет содержимое столбца и с предыдущего временного слоя вычисленными значениями неизвестной функции со следующего слоя. Первые пять строк листинга 13.3 представляют так называемый обратный ход прогонки, а последние две строки – ее прямой ход. Заинтересовавшемуся читателю предлагается самому оформить представленный алгоритм прогонки в виде программы решения разностных уравнений для вычисления произвольного временного слоя по примеру листингов 13.1 и 13.2. Заметим, что описание этого знаменитого алгоритма можно отыскать практически в любом современном учебнике по численным методам.
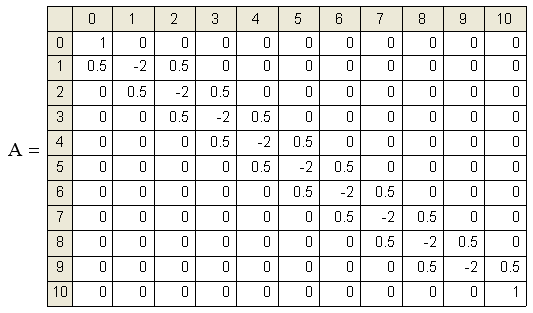
Рис. 13.13. Матрица системы линейных разностных уравнений для неявной схемы (листинг 13.2 для М=10)