Пример: линейное программирование
Задачи поиска условного экстремума функции многих переменных часто встречаются в экономических расчетах для минимизации издержек, финансовых рисков, максимизации прибыли и т. п. Целый класс экономических задач оптимизации описывается системами линейных уравнений и неравенств. Они называются задачами линейного программирования. Приведем характерный пример так называемой транспортной задачи, которая решает одну из проблем оптимальной организации доставки товара потребителям с точки зрения экономии транспортных средств (листинг 6.6).
Листинг 6.6. Решение задачи линейного программирования:
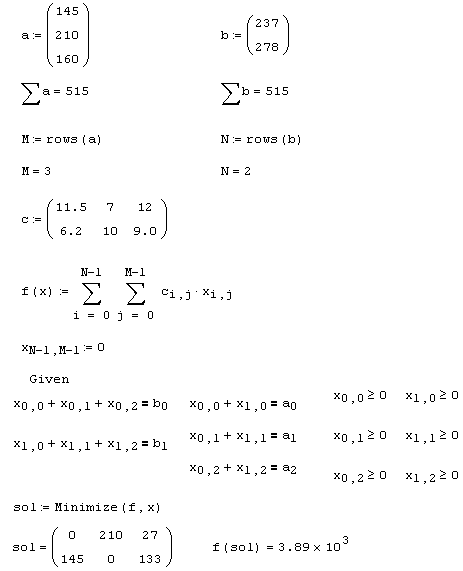
Модель типичной транспортной задачи следующая. Пусть имеется N предприятий-производителей, выпустивших продукцию в количестве b 0,…,bN-1 тонн. Эту продукцию требуется доставить м потребителям в количестве а0,… "а M-1 тонн каждому. Численное определение векторов а и b находится в первой строке листинга. Сумма всех заказов потребителей ai равна сумме произведенной продукции, т. е. всех bi (проверка равенства во второй строке). Если известна стоимость перевозки тонны продукции от i – го производителя к j – му потребителю C i, j, то решение задачи задает оптимальное распределение соответствующего товаропотока xi , j с точки зрения минимизации суммы транспортных расходов. Матрица с и минимизируемая функция f (х) матричного аргумента х находятся в середине листинга 6.6.
Условия, выражающие неотрицательность товаропотока, и равенства, задающие сумму произведенной каждым предприятием продукции и сумму заказов каждого потребителя, находятся после ключевого слова Given. Решение, присвоенное матричной переменной sol, выведено в последней строке листинга вместе с соответствующей суммой затрат. В строке, предшествующей ключевому слову Given, определяются нулевые начальные значения для х простым созданием нулевого элемента матрицы x N-1,M-1.
Примечание 1
Если взять другие начальные значения для х, решение, скорее всего, будет другим! Возможно, вы сумеете отыскать другой локальный минимум, который еще больше минимизирует транспортные затраты. Это еще раз доказывает, что задачи на глобальный минимум, к классу которых относится линейное программирование, требуют аккуратного отношения в смысле выбора начальных значений. Часто ничего другого не остается, кроме сканирования всей области начальных значений, чтобы из множества локальных минимумов выбрать наиболее глубокий.
Примечание 2
Не забывайте о том, что в вычислительном блоке в качестве неизвестных следует использовать все компоненты вектора х, как это сделано в предпоследней строке листинга 6.6 (с/и. разд. 5.1.1). Иными словами, нельзя задавать некоторые из компонент х в виде параметров.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Примечание 3
Еще раз напомним, что в новых версиях Mathcad (начиная с 11-й) появилась возможность программного управления глобальной минимизацией. Для этого служит параметр численного алгоритма Multistart (Сканирование), который следует установить в положение Yes (Да) для поиска глобального экстремума (см. разд. 5.3.2). Любопытно, что если при решении нашей задачи поменять только эту опцию функции Minimize, то численный метод даст сбой, и вместо решения появится сообщение об ошибке. Однако если вспомнить, что наша транспортная задача – линейная, и выставить в контекстном меню, вызываемом на имени функции Minimize, флажок Linear (Линейный), задающий линейный вариант алгоритма, то глобальное решение будет найдено.
