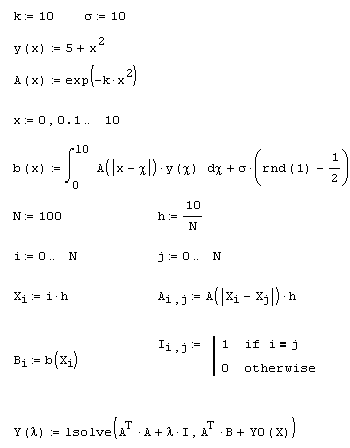Регуляризация Тихонова
Говоря о некорректных задачах, нельзя не отметить, что для их решения советским математиком Тихоновым был предложен чрезвычайно эффективный метод, называемый регуляризацией и основанный на привлечении дополнительной априорной информации о решении, которая может быть как качественной, так и количественной. Например, можно искать решение, максимально близкое к некоторому профилю, т. е. к некоторому вектору Y0. Концепция регуляризации сводится к замене исходной некорректной задачи на задачу о минимизации следующей функции:
Ω(Y, λ) = | AY - B | + λ| Y - Y0 |, (6.5)Где λ – малый положительный параметр регуляризации, который необходимо подобрать определенным способом. Отметим, что, если рассматривать не дискретную, а непрерывную задачу (т. е. профиль у(х) вместо вектора Y), то Ω (у(х),λ) будет представлять собой не функцию, а функционал, исторически называемый функционалом Тихонова.
Минимизируя функцию Ω(Y,λ), можно получить регуляризованное решение Y (А), зависящее от параметра λ. Из (6.5) хорошо ясен его смысл: при малых λ ~ 0 проблема поиска функционала близка к (некорректной) исходной задаче, а при больших А, задача поставлена корректно, но ее решение далеко от решения исходной обратной задачи. А именно, чем больше параметр регуляризации, тем ближе решение к априорной оценке Y0. Очевидно, что на практике необходимо выбирать промежуточные λ.. Можно показать, что в линейном случае задача о минимизации функционала Ω (Y,λ) может быть сведена к следующей системе линейных алгебраических уравнений (решению линейных систем посвящена глава 8):
(AT A+λI)Y=AT B+λY0. (6.6)
Примечание
В общем (нелинейном) случае минимизация Ω (Y,λ) должна производиться по всем компонентам вектора Y, что представляет собой довольно громоздкую вычислительную задачу. Как уже отмечалось, поиск глобального экстремума осложняется не только благодаря многомерности задачи, но и из-за возможности существования нескольких локальных минимумов.
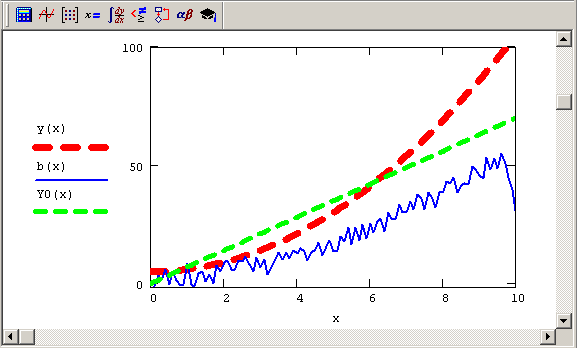
Рис. 6.10. Исходный сигнал Y, его априорная оценка 0 и измерения В (продолжение листинга 6.16)
Приведем в качестве примера применения регуляризации (листинг 6.16) решение некорректной линейной задачи интерпретации измерений, которая решалась нами ранее другими способами в листингах 6.13-6.15. В качестве модельного сигнала будем использовать квадратичную параболу, а в качестве априорной оценки – линейный профиль Y0 (рис. 6.10). Сделаем мы это для того, чтобы соблюсти честность, пытаясь подогнать регуляризованное решение не к исходной (вообще говоря, неизвестной) модели, а к иной зависимости. В результате решения (в последней строке листинга) системы линейных уравнений (6.6), зависящей от А. как от параметра, получается зависимость регуляризованного решения (вектора Y) от X. Соответствующая невязка системы уравнений δ(λ) = |AY(λ)-B|, также являющаяся функцией X, показана на рис. 6.11.
Листинг 6.16. Регуляризация некорректной линейной задачи:
