Пример: регуляризация некорректных задач. О постановке некорректных задач.
Еще один широко распространенный круг задач на решение систем уравнений, называемых обратными, наиболее типичен для современной экспериментальной физики. Значительную часть обратных задач относят к классу некорректно поставленных (или просто некорректных), которые, благодаря своей принципиальной неустойчивости, требуют специального подхода. Как правило, общим принципом решения некорректных задач является их регуляризация, заключающаяся в их сведении к задаче минимизации.
Рассмотрим сначала типичную постановку обратных задач, а затем обратимся к обсуждению корректности их постановки.
Обратные задачи
Строго говоря, обратные задачи связаны, как правило, не с отысканием значения корня уравнения (или системы) f(x)=0, а с вычислением неизвестной функции у (х), описываемой уравнением:
S[y(x)] = b(x), (6.1)Здесь A [у] – некоторый функционал (т. е. функция от функции), а b (х) – известная функция (правая часть уравнения).
Рассмотрим типичную постановку обратных задач на примере так называемой инструментальной задачи. Пусть имеется некоторый сигнал у(х), который подвергается измерению на приборе, условно обозначаемом S. Физику-исследователю доступно измерение данного сигнала, которое находится на выходе прибора (дисплее, табло и т.п.). Обозначим это измерение b (х). Поскольку прибор вносит в сигнал, во-первых, искажения (например, в устройствах типа спектрометров часто измеряются некоторые интегральные характеристики сигнала) и, во-вторых, шумовую компоненту. Формально данную физическую модель можно записать равенством (6.1), в котором оператором s обозначается аппаратная функция, т. е. действие прибора на сигнал у (х).
Листинг 6.13. Пример моделирования прямой задачи, выражающей линейную схему измерений:
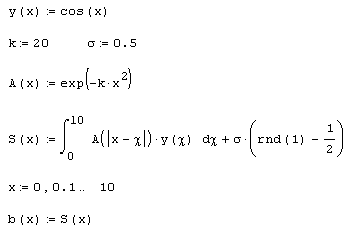
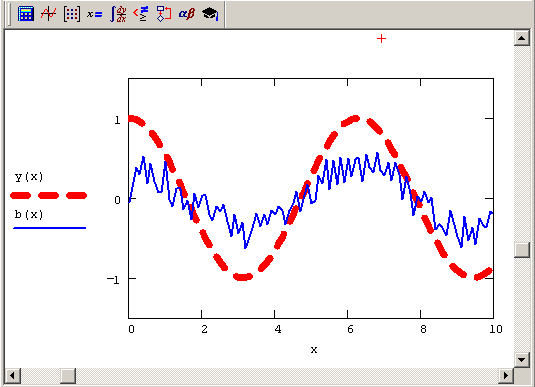
Рис. 6.6. Исходный сигнал и показания прибора (продолжение листинга 6.13)
