Регуляризация Тихонова
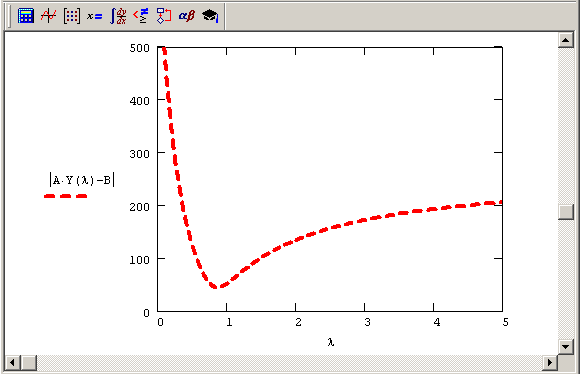
Рис. 6.11. Невязка δ(λ), даваемая регуляризованным решением Y(λ) задачи (6.6) (продолжение листинга 6.16)
Для реконструкции можно использовать такое значение λ, которое соответствует глобальному минимуму зависимости δ(λ). Иными словами, необходимо решить еще одну задачу на минимум, но уже другой функции δ(λ) (листинг 6.17). Подчеркнем, что само определение этой функции подразумевает вложенную минимизацию функционала Тихонова (6.5), которую мы, правда, оформили посредством решения системы линейных уравнений (6.6). Таким образом, для построения реконструкции сигнала (она показана на рис. 6.12) нам пришлось решить две задачи минимизации.
Примечание
Часто применяют и другой способ определения А, называемый принципом невязки. Он подразумевает выбор параметра регуляризации, с которым невязка приблизительно равна сумме погрешностей измерений (т. е. заданий правой части) и аппроксимации (погрешности, заложенной в матрице А).
Листинг 6.17. Квазиоптимальный выбор параметра регуляризации (продолжение листинга 6.16):
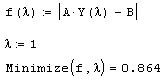
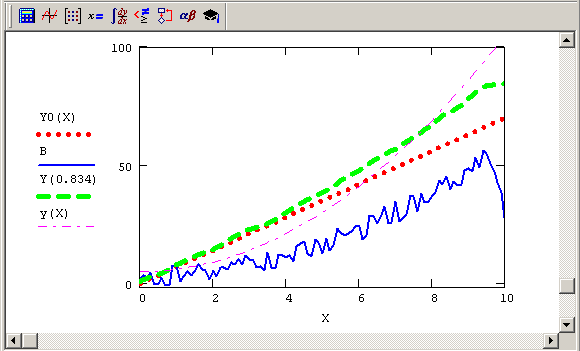
Рис. 6.12. Исходный сигнал Y и его регуляризованная реконструкция (продолжение листинга 6.17)
