Простейшие матричные операции. Транспонирование.
Задачи линейной алгебры, решаемые в Mathcad, можно условно разделить на два класса.
Первый – это простейшие матричные операции, которые сводятся к определенным арифметическим действиям над элементами матрицы. Они реализованы в виде операторов (см. разд. 7.1 и 7.2) и нескольких специфических функций, предназначенных для создания, объединения, сортировки, получения основных свойств матриц и т. п. (см. разд. 7.4). Второй класс – это более сложные действия, которые реализуют алгоритмы вычислительной линейной алгебры, такие как вычисление определителей и обращение матриц (см. разд. 7.3), вычисление собственных векторов и собственных значений, решение систем линейных алгебраических уравнений и различные матричные разложения (см. главу 8).
Простейшие операции матричной алгебры реализованы в Mathcad в виде операторов, причем их запись максимально приближена к математическому значению. Каждый оператор выражается соответствующим символом. Некоторые операции применимы только к квадратным матрицам NxN, некоторые допускаются только для векторов (например, скалярное произведение), а другие, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.
Транспонирование
Транспонированием называют операцию, переводящую матрицу размерности MxN в матрицу размерности NxM, делая столбцы исходной матрицы строками, а строки – столбцами. Несколько примеров транспонирования приведены в листинге 7.1. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш CTRL +!. Не забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.
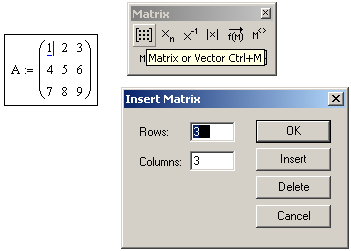
Рис. 7.1. Ввод матриц и основные операции над ними осуществляются при помощи панели Matrix
Примечание
Все матричные и векторные операторы, о которых пойдет речь, допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными. Смело используйте символьный процессор в качестве мощного математического справочника, когда вы хотите вспомнить какое-либо определение из области линейной алгебры. Именно по этой причине мы прибегаем к примерам символьных расчетов в большинстве иллюстраций к данному разделу.
Листинг 7.1. Транспонирование векторов и матриц:
