Вспомогательные матричные функции. Автоматическая генерация матриц.
Перечислим основные встроенные функции, предназначенные для облегчения работы с векторами и матрицами. Они нужны для создания матриц, слияния и выделения части матриц, получения основных свойств матриц и т. п.
Самым наглядным способом создания матрицы или вектора является применение первой кнопки панели инструментов Matrix (Матрицы). Однако в большинстве случаев, в частности, при программировании сложных проектов, удобнее бывает создавать массивы с помощью встроенных функций.
Создание матриц на основе некоторой функции
Наиболее удобный прием автоматизации создания матриц заключается в предварительном определении функции f(i,j), аргументом которой должны быть индексы элементов матрицы:
- matrix (м, N, f) – создание матрицы размера MхN, каждый i,j элемент которой есть f (i, j) (листинг 7.20):
- M – количество строк матрицы;
- N – количество столбцов матрицы;
- f(i,j) – функция.
Листинг 7.20. Создание матрицы на основе функции пользователя:
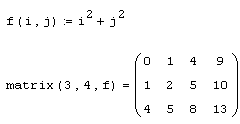
Создание матриц для построения 3D графиков
Для создания матриц имеются еще две специфические функции, применяемые, в основном, для быстрого и эффектного представления каких-либо зависимостей в виде трехмерных графиков (типа поверхности или пространственной кривой). Все их аргументы, кроме первого (имени функции), необязательны. Рассмотрим первую из этих встроенных функций.
- CreateSpace(F(или fI, f2, f3) , t0,t1,tgrid,fmap) – создание вложенного массива, представляющего х-, у- и z-координаты параметрической пространственной кривой, заданной функцией F:
- F(t) – векторная функция из трех элементов, заданная параметрически относительно единственного аргумента t;
- f1(t),f2 (t), f3 (t) – скалярные функции;
- t0 – нижний предел t (по умолчанию -5);
- t1 – верхний предел t (по умолчанию 5);
- tgrid – число точек сетки по переменной t (по умолчанию 20);
- fmap – векторная функция от трех аргументов, задающая преобразование координат.
Пример использования функции CreateSpace показан на рис. 7.2. Заметьте, для построения графика кривой не потребовалось никакого дополнительного кода, кроме определения параметрической зависимости в вектор-функции F!
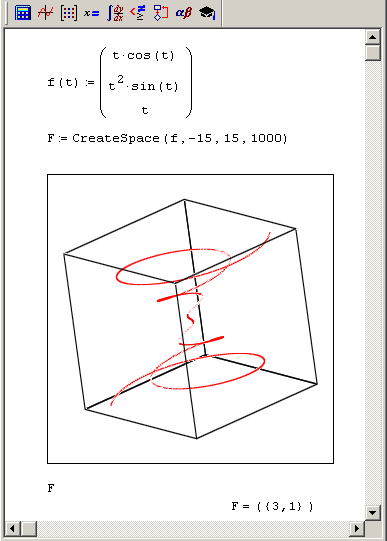
Рис. 7.2. Использование функции CreateSpace для построения графика трехмерной кривой
