Пример: регуляризация некорректных задач. О постановке некорректных задач.
Некорректные задачи
При решении обратных задач важную роль играет их устойчивость. Задача устойчива, если малым флуктуациям правых частей, т. е. вектора в, соответствуют малые флуктуации решения Y. Иными словами, устойчивость по правой части состоит в требовании, чтобы решения близких задач AY=B и AY=B+σB мало отличались друг от друга. Если задача изначально является неустойчивой, то решать ее нет смысла, поскольку погрешности алгоритмов, накапливающиеся в ходе решения численными методами, неизбежно приведут к тому, что будет найдено неверное решение.
Как правило (в том числе в нашем примере), обратные задачи характеризуются наличием шумов, что может быть символически отражено равенством (если опять-таки предположить, что шум ст входит в схему измерений линейно):
AY + σ = B, (6.3)Наличие шума коренным образом меняет идеологию решения обратных задач. Если сама задача является устойчивой, то существование шума может эту устойчивость нарушать. Попросту говоря, различные (даже очень сильно отличающиеся) сигналы Y1 и Y2 могут, будучи искажены шумом, приводить к очень похожим измерениям В1~B2. Поэтому встает вопрос, можно ли извлечь из измерений полезную информацию о сигнале, если наличие шума делает задачу неустойчивой? Такие задачи называются задачами, поставленными некорректно, и для их решения развиты специальные методы, основанные на привлечении дополнительной априорной информации о решении Y, которые будут рассмотрены ниже. Следует также отметить, что класс некорректных задач шире класса обратных (один из примеров вы найдете в конце разд. 11.1.2).
Сказанное иллюстрирует рис. 6.8, на котором представлена попытка решения задачи листингов 6.13 и 6.14 "в лоб", прямым обращением матрицы А. Реконструкция сигнала путем простого обращения матрицы А оказывается возможной лишь для очень низких значений уровня шума а, а при увеличении шума решение Y=A-1 B оказывается совершенно нефизическим. Очевидно, что для получения осмысленного результата следует применять иные методы.
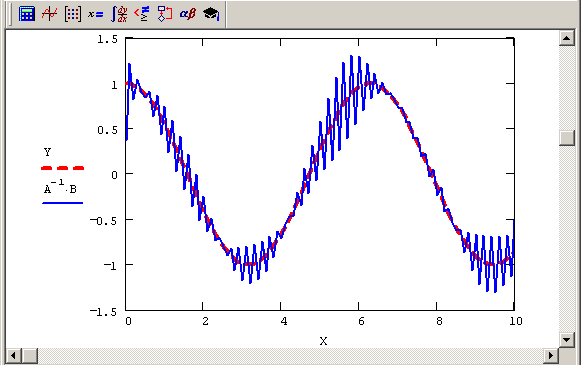
Рис. 6.8. Исходный сигнал и попытка его реконструкции А-1 В (продолжение листингов 6.13 и 6.14) для σ=10-5
Примечание
Проблемы, возникающие при попытке обращения матрицы А, связаны с ее плохой обусловленностью. Подход к подобным задачам может быть не обязательно таким, как рассказывается в двух следующих разделах (см. главу 8).
