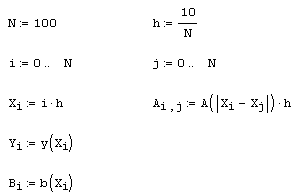Пример: регуляризация некорректных задач. О постановке некорректных задач.
Согласно изложенной модели, измерения b (х) могут довольно сильно отличаться от исходного сигнала у(х), что иллюстрируется простым примером листинга 6.13 и рис. 6.6. В первой строке листинга выбирается модельный сигнал у(х), а во второй и третьей – определяется оператор S [y(x)]. Важно отметить, что использованная структура оператора – интегральная зависимость от сигнала у (х) в сумме с шумовой компонентой – наиболее типична для инструментальных обратных задач. Читателю будет очень полезно "поиграть" с параметрами задачи k и сигма (эффективной шириной спектральной характеристики прибора и интенсивностью шума соответственно), чтобы "почувствовать" специфику модели измерений. Несколько примеров расчетов b (х), согласно листингу 6.13, приведено на рис. 6.7 в виде коллажа нескольких графиков.
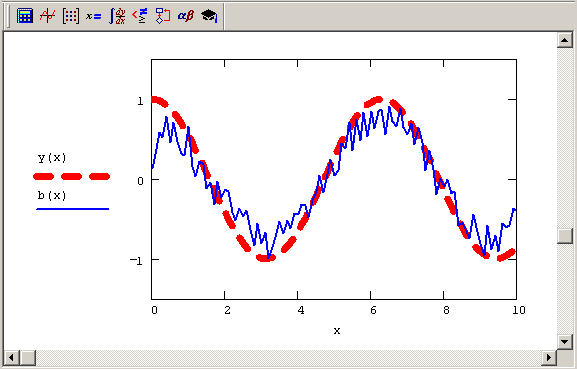
Рис. 6.7. Расчеты показаний прибора (коллаж результатов листинга 6.17 для различных сочетаний параметров k и 0)
Примечание 1
Модель измерений, представленная в третьей строке листинга 6.13, описывает, с математической точки зрения, типичное интегральное уравнение, в которое неизвестная функция у(х) входит в виде части подынтегральной функции. Класс обратных задач чаще всего (но не всегда) соответствует как раз интегральным уравнениям.
Примечание 2
Неизвестная функция у (х) входит в модель, приведенную в листинге 6.13, линейным образом (в первой степени под знаком интеграла). В связи с этим рассматриваемая задача является линейной, а саму модель называют часто линейной схемой измерений. Линейность модели проявляется также в том, что ее дискретная форма записывается в виде матричного соотношения (см. листинг 6.14 ниже).
Из сказанного выше понятно, что в практических приложениях весьма актуальна задача восстановления сигнала у(х) по показаниям прибора b (х) (при наличии определенной дополнительной информации о физике измерения, т. е. об операторе S, выражающем действие прибора). Таким образом, в отличие от прямой задачи, выражающейся равенством (6.1), обратной задачей является восстановление функции у (х) по известной b (х).
Обычно сигнал (и, соответственно, его измерение) может зависеть от времени и/или пространственных координат. Эту зависимость мы обозначили как зависимость от х. При использовании численных методов непрерывные зависимости от х дискретизируются, заменяясь соответствующими векторами. Таким образом, задача отыскания неизвестной функции у(х) заменяется задачей поиска неизвестного вектора Y и может быть записана в матричном виде:
S(Y) = B, (6.2)Здесь вектор у неизвестен, а оператор S (в линейном случае S(Y)=AY, где А – матрица) и вектор правых частей уравнений в известны. Таким образом, в дискретном случае обратная задача для рассматриваемой математической модели состоит в решении системы (в общем случае, нелинейных) уравнений (6.2). Построенная описанным способом дискретная задача представлена в листинге 6.14. Важно отметить, что, поскольку исходная задача линейна, дискретный вариант ее оператора записывается в виде матрицы А, а сама задача сводится к системе линейных алгебраических уравнений AY=B.
Примечание
Рекомендуем читателю обратиться к соответствующему файлу Mathcad на прилагаемом к книге компакт-диске и сравнить графики сигнала и измерений, соответствующие непрерывной (интегральной) и дискретной (матричной) модели. Будет очень полезным осуществить расчеты для разных значений параметров, в том числе количества точек дискретизации м, а также разобраться, какова структура матрицы А.
Листинг 6.14. Дискретная форма прямой задачи линейной модели измерений (продолжение листинга 6.13):
