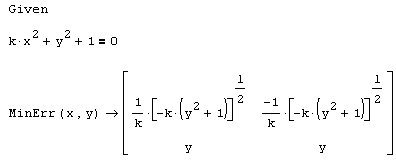Иллюстрированный самоучитель по MathCAD 12

Приближенное решение алгебраических уравнений

Пока мы рассматривали пример нахождения существующего решения уравнения. Приведем теперь пример нахождения функцией Minerr приближенного решения не имеющего корней уравнения (листинг 6.10), а также несовместной системы уравнений и неравенств (листинг 6.11). Решение, выдаваемое функцией Minerr, минимизирует невязку данной системы. Как видно из листингов, в качестве результата выдаются значения переменных, наилучшим образом удовлетворяющие уравнению и неравенствам внутри вычислительного блока.

Внимание!
Полученное в листинге 6.11 решение не удовлетворяет неравенствам, составляющим задачу. Это и неудивительно, поскольку точного решения системы нет, и в качестве ответа Mathcad выдает значения аргументов, минимизирующих норму общей невязки (не отдавая предпочтения ни уравнению, ни неравенствам).

Листинг 6.10. Приближенное решение уравнения x² +y² +1=0:

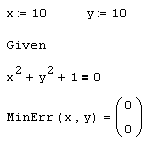
Листинг 6.11. Приближенное решение несовместной системы уравнений и неравенств:

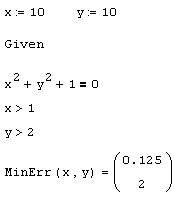
Внимательный читатель может обнаружить, что решение, выдаваемое функцией Minerr в рассматриваемом примере, не является единственным, поскольку множество пар значений (х,у) в равной степени минимизирует невязку данной системы уравнений и неравенств. Поэтому для различных начальных значений будут получаться разные решения, подобно тому, как разные решения выдаются функцией Find в случае бесконечного множества корней (см. разд. 5.2.4). Еще более опасен случай, когда имеются всего несколько локальных минимумов функции невязки. Тогда неудачно выбранное начальное приближение приведет к выдаче именно этого локального минимума, несмотря на то, что другой (глобальный) минимум невязки может удовлетворять системе гораздо лучше.

В завершение раздела сделаем очень важное замечание, связанное с возможностью использования встроенной функции Minerr в символьных расчетах. Как и функция решения алгебраических систем Find, она может применяться без предварительного присвоения каких-либо начальных значений любым переменным, входящим в уравнение, как это проиллюстрировано листингом 6.12, решающим ту же самую задачу аналитически. Замечательно, что в результате получается не одно решение, а все семейство решений, одинаково минимизирующее невязку.

Листинг 6.12. Аналитическое приближенное решение уравнения kx² +y² +1=0: