Квазирешение
Одним из наиболее простых методов решения некорректных обратных задач является концепция поиска их квазирешения. Рассмотрим обратную задачу AY=B, где неизвестный вектор Y подлежит определению, а оператор (в линейном случае, матрица) А и вектор правых частей уравнений в известны. Подчеркнем, что задача может быть и нелинейной, т. е. оператор А может описывать сложную зависимость.
Основная идея квазирешения состоит в параметризации неизвестного вектора Y, исходя из физических соображений постановки задачи. То есть на основе некоторой имеющейся априорной информации следует заранее задать модельный вид Y~Y0, зависящий от ряда параметров r1,r2,… В результате пространство поиска решений значительно сужается – вместо отыскания всех компонент вектора Y требуется лишь найти значения модельных параметров, решающих (в определенном смысле) задачу.
Квазирешение Y0 находится из решения задачи на минимум:
r = arg min(IA - YO(r) - B), (6.4)Здесь минимизация проводится по вектору S параметров модельной зависимости Y0 (r). Следует подчеркнуть, что задача поиска квазирешения является задачей на глобальный экстремум, что важно с позиций выбора вычислительного метода (как уже отмечалось, наиболее популярны градиентные методы поиска минимума в комбинации со сканированием для достижения глобальной минимизации – алгоритмами сплошного или случайного поиска).
Пример отыскания квазирешения обсуждавшейся в предыдущих разделах задачи приведен в листинге 6.15 и на рис. 6.9 (данные о результатах модельных измерений в и матрице А взяты из предыдущего листинга). Понятно, что при сведении некорректной задачи к проблеме отыскания квазирешения решающее значение принадлежит правильно выбранной параметризации неизвестного вектора у.
Листинг 6.15. Квазирешение некорректной задачи (продолжение листингов 6.13 и 6.14):
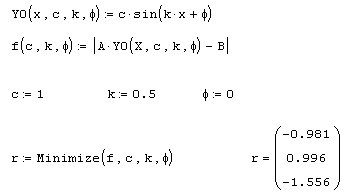
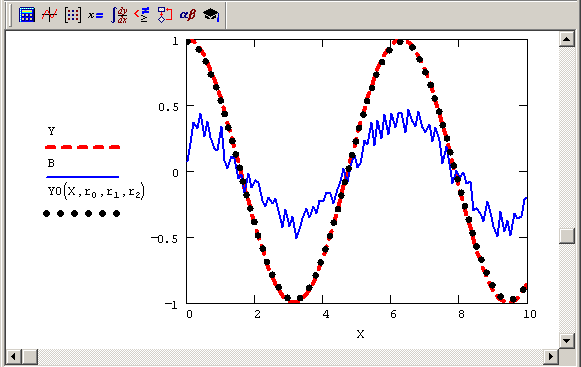
Рис. 6.9. Исходный сигнал У, измерения В и квазирешение Y0 (продолжение листинга 6.15)
