Знакомство с символьными вычислениями. Особенности систем компьютерной математики.
Так чему равна сумма квадратов синуса и косинуса?
Попытка вычислить в общем виде выражение sin(x)2 + соs(x)2 с помощью численных математических систем или программ на обычных языках программирования к успеху не приведет. Вместо ожидаемого результата появится сообщение об ошибке вида: "Переменная х не определена!". Компьютер будет ждать ввода конкретного значения для х.Так будет независимо от того, запрограммировали вы вычисления на простеньком Бейсике или на языке профессионалов-программистов C++. И лишь системы символьной математики при вычислениях дадут долгожданное и абсолютно точное значение 1 (рис. 1. 3).
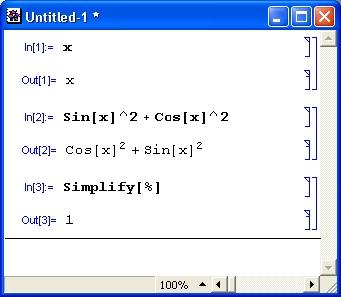
Рис. 1.3. Система Mathematical вычисляет значение sin(x)2 +cos(x)2
Пока не стоит обращать внимание на то, как получен рис. 1.15 – это окно реально работающей системы Mathematica. Уже при рассмотрении простейшего примера, представленного на этом рисунке, можно сделать несколько характерных выводов. Прежде всего видно, что при выводе неопределенной переменной х мы получаем просто имя этой переменной. Функции sin(х) и cos(х) в системе Mathematica обозначаются как Sin [х] и Cos [х]. Само по себе выражение sin(х)2 + cos(х)2 просто повторяется, а для его вычисления используется функция Simplify (упростить), аргументом которой является знак %, означающий подстановку предшествующего выражения. Два знака % можно использовать для подстановки предшествующего предшествующему выражению и т. д. Для вычисления строки ввода надо нажимать клавиши SHIFT + Enter, нажатие же одной клавиши Enter просто переводит строку в области ввода, именуемой также ячейкой ввода.
Любопытно, что в начале запуска, сопровождаемого музыкальным звуком, Mathematica выводит чистое окно редактирования документа, в котором нет даже маркера ввода – характерной вертикальной черточки. Этот маркер появится, как только вы введете какой-то первый символ. После получения первого результата появляется и длинная горизонтальная черта, отделяющая выведенные ячейки от свободного поля окна редактирования под ними. Эта черта является признаком возможности ввода очередной ячейки. Ее можно перевести в уже созданную область документа, если вы захотите создать новую ячейку среди уже существующих ячеек ввода.
Обратите внимание на то, что система выделяет ячейки ввода определителем In [N], а ячейки вывода – определителем Out [N], где N – автоматически проставляемый номер строки. Кроме того, в левой части отображаются квадратные скобки с особыми признаками, которые будут описаны в позже. Далее мы, как правило, будем опускать определители ячеек и квадратные скобки и представлять документы в упрощенной и более компактной форме. Например, представленный на рис. 1.15 документ может быть записан в следующем виде:
x x Sin[x] ^ 2 + Cos[x] ^ 2Cos[x] 2 + Sin[x] 2Simplify[%] 1Здесь входные выражения задаются жирным прямым шрифтом, а выходные – прямым шрифтом обычной насыщенности, то есть именно так, как они выглядят при настройке системы по умолчанию. При этом выходные выражения имеют обычный (в терминах системы Mathematica – стандартный) вид, присущий математическим формулам. Все такие выражения в книге представлены путем копирования ячеек ввода и вывода в текст с помощью буфера обмена (Clipboard). Технология такого копирования и ее особенности будут описаны далее.
Ячейки нумеруются по мере их использования. При этом можно с конца документа вернуться к его началу или середине и, изменив содержимое ранее использованных ячеек, снова выполнить вычисления. При этом ячейки меняют номера. При загрузке файла ячейки перенумеруются в строго последовательном порядке. Таким образом, номера ячеек не являются жестко фиксированными, они представляют собой сугубо техническое средство, отражающее работу системы в текущем сеансе-сессии. Это говорит в пользу отказа от вывода определителей ячеек при записи большинства примеров.