Диалог с системой и ее входной язык
Чем дальше в лес, тем больше дров!
К сожалению, в математике нередко оказывается так, что результирующие выражения быстро нарастают по сложности при, казалось бы, незначительном усложнении или просто изменении условий задачи. Покажем это на примере решения одной из самых часто встречающихся задач – поиска в аналитическом виде корней алгебраического уравнения с целыми степенями членов.
Многие из нас прекрасно помнят формулы для корней квадратного уравнения, которые нам давали еще в школе. Их в точности воспроизвела Mathematica в одном из примеров, приведенных в этом уроке чуть ранее. Это решение еще раз воспроизведено на рис. 1.7 (сверху).
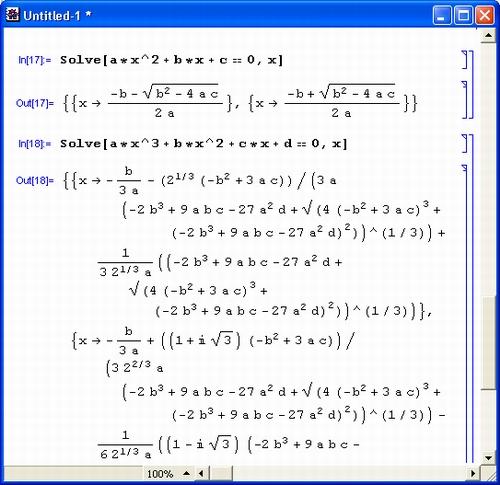
Рис. 1.7. Система Mathematica решает квадратное и кубическое уравнения
Однако едва ли кто вспомнит по памяти формулы аналитического решения кубического уравнения общего вида. Зато система Mathematica играючи справляется с этой задачей с помощью функции Solve, что и показано во втором примере на рис. 1.19. Полученное выражение впечатляет даже студентов университетов, уже изучивших курс математики в полном объеме. Это блестящий пример эффективного представления справочной информации.
Можно пойти чуть дальше и убедиться в том, что Mathematica решает подобное уравнение даже четвертого порядка. Полученное при этом крайне громоздкое решение (в силу этого оно не приводится) заставит в задумчивости почесать затылок многих любителей математики. Но можно ли продолжать эти вычисления? Увы, классическая математика говорит, что нет! Подобные уравнения порядка выше четвертого современная математика в аналитическом виде не решает. Тем не менее, попытаемся вычислить корни алгебраического уравнения пятой степени в общем виде (рис. 1. 8).
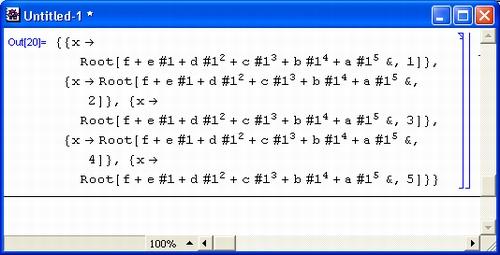
Рис. 1.8. Система Mathematica пытается решить алгебраическое уравнение пятой степени
А вот и сюрприз: Mathematica не только не отказалась решать эту задачу (при отказе она просто повторяет вводимое выражение), но даже подсказала путь ее решения с помощью пятикратного применения функции вычисления корней Root степенных многочленов.
В упомянутых примерах мы сталкиваемся с одной из серьезных проблем символьной математики – разбуханием результатов аналитических преобразований при порой незначительном усложнении решаемых задач. В данном случае это никоим образом не является недостатком систем компьютерной математики как таковых – просто так нарастает сложность решения данной математической задачи в соответствии с канонами абстрактной математики.
Однако нередко разбухание результатов кроется в сложности алгоритмов, особенно рекурсивных. Современные системы символьной математики способны осуществлять весьма глубокую рекурсию, и порой трудно даже предположить, к сколь громоздкому результату это в конечном счете приведет.
