Иллюстрированный самоучитель по Mathematica 3/4

Диалог с системой и ее входной язык

Научные работники и инженеры настолько привыкли к упрощению (порой весьма грубому, с точки зрения математиков), что громоздкие решения, получаемые с помощью систем символьной математики, способны их раздражать. Это в определенной мере препятствует применению систем символьной математики на практике и в наши дни.

Однако для частных случаев нередко можно получить вполне сносные по виду решения. Вот пример решения неполного алгебраического уравнения десятой степени, при котором Mathematica благополучно возвращает все десять корней довольно простого вида (рис. 1.9).

Примеры такого рода можно встретить повсеместно. Есть множество нелинейных алгебраических или дифференциальных уравнений обманчиво простого вида, но имеющих сложнейшие решения или не имеющих их вовсе. Так что если система символьной математики не находит ответ, это зачастую не является признаком ее слабости – может быть, решения не существует вообще? Порой даже такой отрицательный результат избавляет пользователя от трудоемкого поиска несуществующих решений "в лоб" и направляет его на поиск обходных, порою весьма ценных и полезных методов решения.

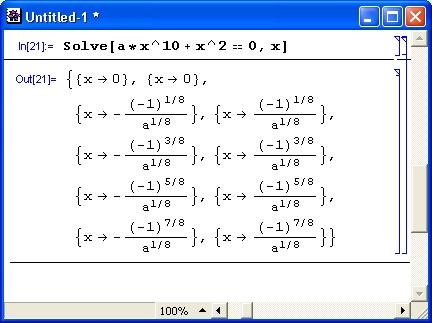
Рис. 1.9. Система Mathematical решает алгебраическое уравнение 10-й степени

Доверяй, но проверяй!

Ситуация с применением математических систем компьютерной алгебры осложняется тем, что они, как и люди-математики, могут давать результаты в различной форме и даже делать ошибки. Вынесенная в заголовок этого подраздела армейская поговорка как нельзя лучше характеризует правильные приемы работы с математическими системами. Если вы получили результат, который не ожидали, – не спешите считать его окончательным и тем более новым. Всегда желательно этот результат сначала проверить. Покажем, как это делается.

Пусть мы решили некоторое уравнение:

И получили его корни:

Для проверки решения можно использовать операцию подстановки в eqns списка корней г. Эта операция реализуется оператором /., что иллюстрирует следующий пример:

Результат этой операции – список из трех логических констант True (Истинно). Он означает, что решение верно. Кстати, с помощью этой подстановки можно получить истинный список корней:

Mathematica имеет и множество иных способов проверки полученных результатов. Но, к сожалению, очень редко встречаются ситуации, когда выданное Mathematica ошибочное или несуществующее решение при подобной проверке дает положительный результат. Как говорится, за что боролись, на то и напоролись! В таких особо каверзных случаях надо ориентироваться на свою интуицию, решение схожей тестовой задачи или решение с помощью других математических систем с иным ядром – например, Derive или Maple V.

Примечание:
Не стоит брезговать проверкой решений даже с помощью менее мощных систем – помните поговорки "Устами младенца глаголет истина!", "Пуля дура – штык молодец", "Мал золотник, да дорог!" и т. д.? Обращайтесь к описанным выше правилам проверки по мере освоения работы с системой Mathematica. При этом вам быстро станут понятными некоторые ее тонкости, которые пока остались "за бортом".