Иллюстрированный самоучитель по Mathematica 3/4

Диалог с системой и ее входной язык

Арифметика произвольной точности

Арифметика произвольной точности – еще одна из областей применения систем символьной математики (рис. 1. 5).

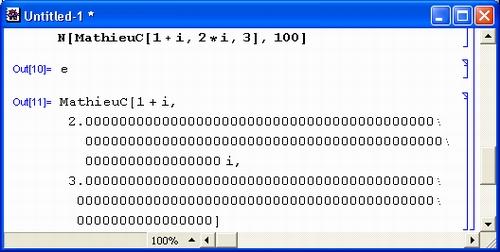
Рис. 1.5. Примеры вычислений с большой точностью

Здесь использована одна из самых распространенных функций системы Mathematica – N[expr, n], дающая результат вычисления выражения ехр r с точностью до n знаков после десятичной точки. Константы я и е вычислены с 500 верными знаками, а новая функция Матье (MathieuC) – с точностью до 200 знаков. Однако в системе Mathematica n может достигать миллиона и более. Ограничения по разрядности чисел и их верхнему и нижнему пределам практически отсутствуют.

Примеры из математического анализа

Разумеется, роль систем символьной математики далеко не исчерпывается приведенными выше примерами. Эти системы способны преобразовывать сложнейшие алгебраические выражения, находить аналитические решения сложных систем линейных, нелинейных и дифференциальных уравнений, манипулировать со степенными многочленами, вычислять производные и интегралы, анализировать функции, находить их пределы и т. д. Это видно уже из примеров, представленных на рис. 1.6.

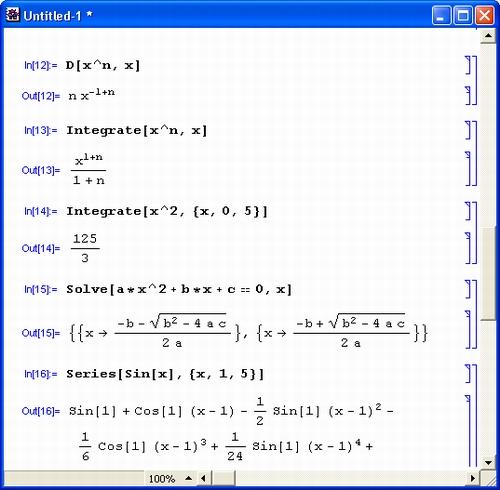
Рис. 1. 6. Примеры вычислений из области математического анализа

В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate – интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).

Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:

Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.