Пакет решения задач линейной оптимизации simplex
Функция dual(f, С, у) имеет следующие параметры: f – линейное выражение y, С – множество неравенств и у – имя. Эта функция возвращает сопряженное с f выражение:
> dual(x-y,{2*x+3*y<=5.3*x+6*y<=15},z);
115zl +5z2, {1_<3z1+2z2,-1_<6z1+3z2}
Функция feasible может быть задана в трех формах:
feasible(C) feasible(C,vartype) feasible(C,vartype,'NewC','Transform')
Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:
> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);
true
> feasib1e({2*x+3*y<-5, 3*х+б*у ← 15}, NONNEGATIVE);
false
Если функция возвращает логическое значение true, то заданная система осуществима, а если false – неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:
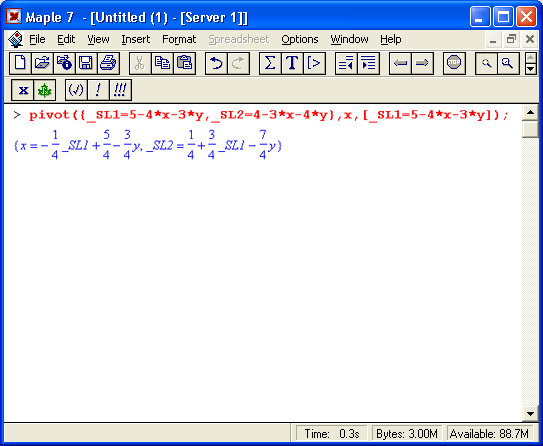
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:
> pivoteqnC {_SL1-5-3*х-2*у. _SL2-4-2*х-2*у}. х);
[_SLl = 5-1x-2y]
