Задачи динамики. Определение траектории движения частицы в однородном стационарном электрическом поле.
Дальше с помощью оператора цикла вычисляем координаты (х- и у-координату) через одну, две и так далее, до десятой секунды. Значения координат записываются в виде списка, и этот список добавляется в качестве элемента в список List, т.е. List является списком списков. Кроме того, следует отметить, что координаты точек нормированы соответствующим образом. Это сделано для того, чтобы точки в дальнейшем можно было отобразить на графике.
Можно просмотреть, как же в конечном счете выглядит список координат (при выполнении предыдущего оператора в области вывода ничего не отображается, поскольку соответствующая команда заканчивается двоеточием, а не точкой с запятой).

Теперь можно построить траекторию движения частицы. Квадратами на этой траектории будем отмечать положения частицы через каждую секунду. При этом первым параметром процедуры plot() указываем список с двумя элементами: первый элемент – это список для отображения заданной в параметрическом виде функции (это и есть траектория частицы), второй – переменная List, которая, как известно, содержит координаты частицы.
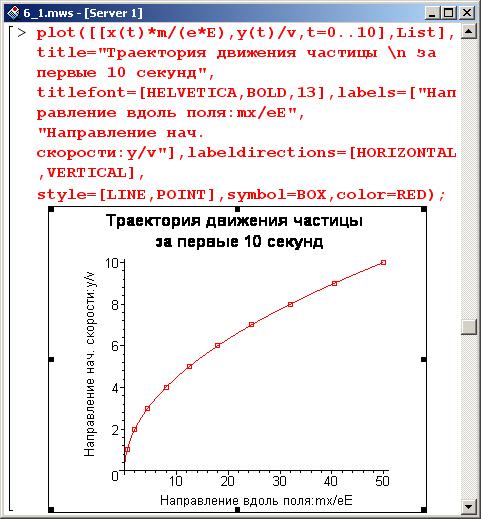
Однако графического отображения траектории мало – нужно определить уравнение этой траектории. Для этого из одной функциональной зависимости следует выразить время через координату и подставить полученное таким образом выражение в другое уравнение.
Чтобы отличить непосредственно координату от функциональной зависимости этой координаты от времени, введем переменные X и Y. Уравнение движения вдоль оси х может быть записано в новых переменных как X=x(t), а вдоль оси у – как Y=y(t).
Из последнего уравнения и выразим время через координату. Сделать это можно посредством команды isolate(Y=y(t),t). Далее выполняем подстановку в оставшемся уравнении с помощью процедуры subs(), указав это уравнение вторым параметром, а процедуру isolate() – первым.
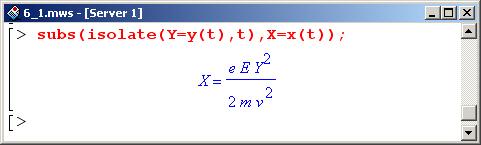
Таким образом, частица, попав в область действия поля, движется по параболе в плоскости, определяемой векторами поля и начальной скорости. Уравнение параболы представлено выше.
