Определение траектории движения частицы в одновременно электрическом и магнитном полях
Однако интересно представить себе, как такая траектория может выглядеть. Поэтому рассмотрим конкретную ситуацию.
В качестве частицы рассмотрим позитрон (то же, что электрон, но с положительным зарядом). Масса такой частицы (в килограммах) приведена ниже.
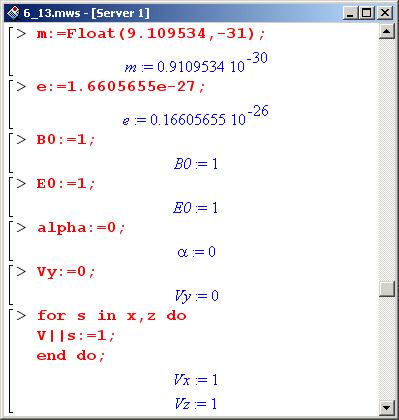
После этого можно строить траекторию частицы. Исследовать будем движение позитрона в течение 0.05 секунды (для позитрона и этого много). Поскольку строить предстоит параметрически заданную кривую в трехмерном пространстве, воспользуемся процедурой spacecurve() из пакета plots. Ее первым параметром является список с параметрическими зависимостями координат частицы вдоль каждой оси от времени, затем указывается интервал изменения параметра (в данном случае это время). Кроме того, указаны задающие ориентацию графика углы (orientation=[30.75]), тип отображаемых координатных осей (axes=FRAMED), число базовых точек (numpoints=200). Остальные опции (толщина и цвет линии, название графика, шрифт для названия) читателю должны быть уже знакомы.
Внимание!
В качестве отображаемых параметрических зависимостей указываются не сами уравнения (Rx.Ry.Rz), а их правые части (rhs(Rx),rhs(Ry),rhs(Rz)).
На заметку
Ориентацию и тип координатных осей можно и не задавать, а просто выбрать их с помощью соответствующей кнопки контекстной панели графики или раскрывающегося меню. Однако это придется делать каждый раз при новом отображении графика.

