Определение траектории движения частицы в одновременно электрическом и магнитном полях
Задача 6.2
В некоторой области пространства одновременно имеются однородные и стационарные электрическое и магнитное поля, угол между которыми а. Частица с массой m и зарядом е, имеющая начальную скорость v, попадает в это пространство. Определить траекторию движения частицы.
Принципиально эта задача мало чем отличается от предыдущей. Ситуация, правда, несколько усложняется из-за наличия магнитного поля. Дело в том, что сила Лоренца (она определяет силу, действующую на частицу со стороны магнитного поля) выражается через векторное произведение. Трудность эта не принципиальна, но вычисления по использованной ранее схеме достаточно громоздки.
В данном случае решать будем векторное уравнение. Для этого понадобится определить две процедуры: для дифференцирования вектора и вычисления векторного произведения.
Процедура дифференцирования вектора (в наиболее простом варианте) выглядит следующим образом.

Данная процедура имеет два параметра – вектор (размерности 3), который и необходимо дифференцировать, и переменную, по которой следует вычислять производную. Процедура возвращает в качестве результата вектор, компоненты которого определяются через производные соответствующих компонентов вектора, указанного первым аргументом процедуры.
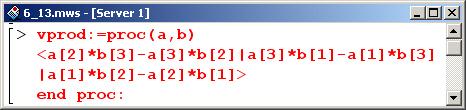
Следующая процедура vprod() нужна для вычисления векторного произведения двух векторов. В соответствии с правилом вычисления такого произведения, в теле процедуры компоненты результирующего вектора определены напрямую через компоненты векторов-параметров процедуры.
Далее следует выбрать систему координат. Начало этой системы разместим в точке, где частица попадает в область действия полей, а сам момент вхождения частицы в данную область выберем за начало отсчета времени.
Ось Y направим вдоль вектора магнитного поля, а ось X – перпендикулярно плоскости векторов электрического и магнитных полей. Тогда проекция вектора электрического поля на ось X равна нулю, а на прочие оси определяется следующим образом.

Поскольку в условии ничего конкретно о направлении вектора начальной скорости не сказано, рассматриваем наиболее общий случай, когда все три проекции вектора начальной скорости отличны от нуля.

Для определения координат частицы введем вектор r, который опишем следующим образом.

Другими словами, r является вектор-функцией, зависящей от времени.
