Вычисление времени сжатия пружины под воздействием упавшего груза
Задача 6.3
Груз массы М падает без начальной скорости с высоты Н на спиральную пружину. Под действием упавшего груза пружина сжимается на величину а. Вычислить время сжатия пружины (массой пружины и силами трения можно пренебречь).
В первую очередь задаем уравнения движения. Поскольку движение одномерное, уравнение будет всего одно. Координатную ось X, вдоль которой и будет двигаться шарик, направим вверх. Точку начала отсчета выберем так, чтобы она соответствовала верхнему свободному концу несжатой пружины (это будет точка 0). В общем виде, согласно второму закону Ньютона, записываем следующее (x(t) – координата шарика в момент времени t).
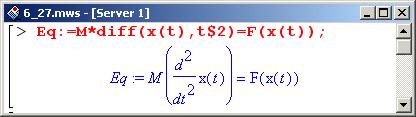
Однако для того, чтобы решить присвоенное в качестве значения переменной Eq уравнение, необходимо задать силу F(x), которая существенно зависит от того, долетел шарик до пружины или нет. Поскольку необходимо вычислить время сжатия пружины, движение шарика будем рассматривать начиная с того момента, когда шарик долетает до пружины. Другими словами, в момент времени t=0, по определению, координата шарика х(0)=0. Это, кстати, будет одним из двух начальных условий (второе – для скорости).
Поэтому равнодействующая двух сил, равная их сумме с учетом направленности, равна следующему.
Последнее выражение определяет действующую на шарик силу как функцию координаты.
Далее, чтобы решить дифференциальное уравнение, необходимо определить еще одно начальное условие для скорости, т.е. необходимо определить скорость в нулевой момент времени – при падении шарика на пружину. Для этого воспользуемся законом сохранения энергии. Поскольку шарик начинал падать с высоты Н без начальной скорости, его полная энергия равнялась потенциальной и была равна М*g*Н.
При падении шарика на пружину потенциальная энергия равна нулю (поскольку система координат выбрана так, что в момент столкновения с пружиной шарик находится на нулевом уровне). Однако кинетическая энергия отлична от нуля. Если скорость шарика в момент столкновения равна v, то кинетическая энергия, с одной стороны, равна M*v*2/2, а с другой – должна быть равна полной энергии М*g*Н. Из этого уравнения находим скорость шарика при столкновении с пружиной.
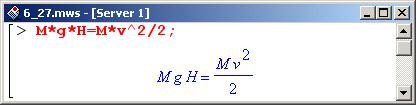
Для решения уравнения используем процедуру solve(), указав, что решать уравнение следует относительно переменной v.
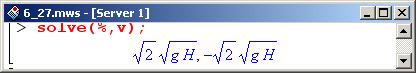
В результате получаем два решения, которые отличаются только знаком. Выражение со знаком "минус" соответствует движению вниз (в направлении, Противоположном направлению координатной оси), а другое, соответственно, – движению вверх. В данном случае очевидно, что шарик движется вниз, поэтому именно отрицательное решение и выбираем (в списке полученных на предыдущем этапе решений оно является вторым).
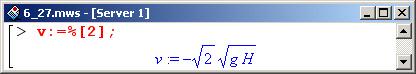
После этого можно решать дифференциальное уравнение Eq.
Если добавить к этому уравнению начальные условия, решение будет определено однозначно (уравнение с начальными условиями – это, как известно, задача Коши).