Вычисление времени сжатия пружины под воздействием упавшего груза
Решаемое уравнение и его начальные условия в процедуре dsolve() заключаются в фигурные скобки.

На заметку
Поскольку начальное значение для скорости – это производная в точке t=0, для записи этого условия (производной) используется оператор D – D(x)(0)=v.
Правую часть полученного выражения, которая и определяет зависимость координаты шарика от времени, обозначим через переменную X.
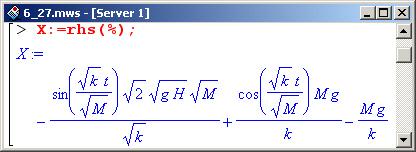
Внимание!
Зависимость X справедлива до тех пор, пока шарик находится в контакте с пружиной. Как только шарик от пружины отскочит, уравнение движения будет иным.
Зависимость скорости шарика от времени определяется через производную по времени от переменной X (которая, напоминаем, является зависимостью координаты шарика от времени).
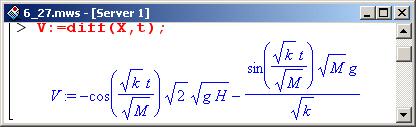
Скорость нам понадобится вот для каких целей. Отсчет времени начинается с момента столкновения шарика с пружиной. Далее пружина сжимается на какую-то граничную величину (в условии задачи это а), после чего начинает разжиматься. Следовательно, время, в течение которого пружина сжимается, [равно по абсолютной величине (при данном выборе начала отсчета времени) моменту, когда пружина прекращает сжатие и начинает разжиматься. Этот |момент характерен тем, что скорость шарика равна нулю!
Отсюда дальнейшие действия очевидны (почти!) – нужно определить момент времени, когда производная от координаты (т.е. скорость) равна нулю. Однако здесь есть один нюанс. Дело в том, что полученное решение исходного уравнения и, соответственно, временная зависимость для скорости, содержат тригонометрические функции. При решении уравнения V=0 относительно t найдены не все решения (в данном случае только на интервале изменения арктангенса, и это решение не будет учитывать периодичность общего решения). Иногда в этом нет ничего страшного, но только не в этом случае. Другими словами, необходимо найти все решения уравнения V=0. С этой целью изменяем значение переменной среды _EnvAllSolutions (переменная определяет, следует искать абсолютно все решения) на true.

Находим момент времени (если точнее, то моменты, но реальный интерес физический смысл имеет только один), в который скорость равна нулю. Решение присваиваем в качестве значения переменной Т.

Здесь переменная _Z1 обозначает любое целое число, поскольку данное сражение описывает общее решение, из которого следует выделить единственное. Определяется оно очень просто – это первое положительное решение. Можно использовать для этого мощный "арсенал" Maple, однако в данном случае поступим проще.
