Вычисление времени сжатия пружины под воздействием упавшего груза
На этом описание процедуры Sys_display() заканчивается. Далее следует определиться с законом движения шарика и, разумеется, пружины.
Выше была вычислена зависимость высоты шарика от времени после падения его на пружину (переменная X). Ниже эта зависимость представлена в виде функции Y(t).
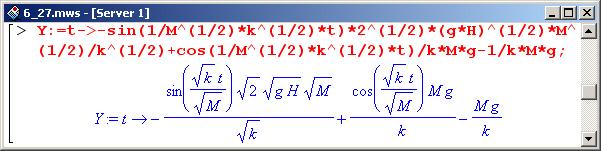
Внимание!
В приведенной выше зависимости время отсчитывается от момента падения шарика на пружину!
Как уже отмечалось ранее, зависимость высоты шарика от времени является "сшивкой" двух зависимостей: первая – это зависимость для свободно падающего шарика, вторая – зависимость для шарика, упавшего на пружину и движущегося далее вместе со сжимающейся пружиной.
Для дальнейшего анализа необходимо определить время свободного падения шарика с высоты Н (как долго шарик падает, прежде чем столкнуться с пружиной). Время это, как известно, равно следующему.
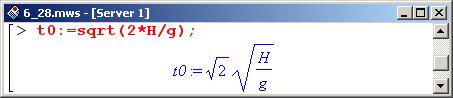
Для большей конкретности зададим такие значения для параметров задачи (хотя это можно сделать и позже) – длина пружины будет равна 5 метрам.

Толщина пружины будет составлять 20% от длины недеформированной пружины, т.е. 1 метр.
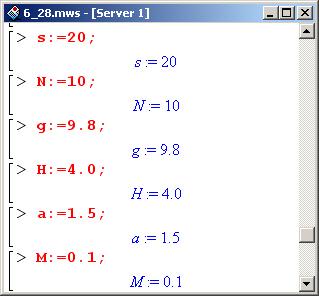
Теперь задаем функциональную зависимость высоты шарика от времени. Зависимость запишем так, чтобы можно было определить положение шарика в произвольный момент времени. Полезными будут следующие рассуждения.
Понятно, что движение шарика (при отсутствии трения) периодично – шарик будет периодически подпрыгивать, падать, ударяться о пружину, сжимать ее, двигаться вверх при разжатии пружины и снова подпрыгивать. Время от прыжка до прыжка (т.е. период), очевидно, равно удвоенному времени свободного падения шарика (t0) и времени сжатия пружины (Т), т.е. период равен 2*(T+t0).
