Вычисление времени сжатия пружины под воздействием упавшего груза
Чтобы восстановить динамику системы, достаточно знать ее динамику на интервале времени от 0 до (T+t0). В силу симметрии уравнений механики и периодичности движения, в произвольный момент времени t положение и скорость шарика могут быть вычислены согласно следующим правилам. Во-первых, от интервала t можно отнять целое число периодов 2*(T+t0), при этом положение и скорость шарика не изменятся. Во-вторых, если t>(T+t0), то положение и модуль скорости шарика будут такими же, как в момент времени 2*(T+t0)-t, но только скорость имеет противоположный знак.
Зависимость, определяющая положение шарика в произвольный момент времени t, описана ниже как процедура h().
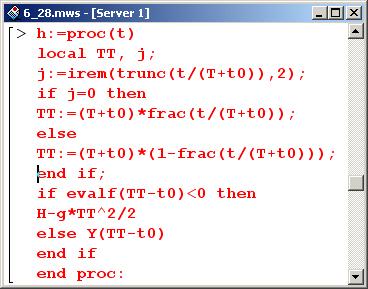
В теле процедуры используются две локальные переменные ТТ и j. В качестве значения переменной j присваивается остаток от целочисленного деления (irem()) результата выполнения операции trunc(t/(T+t0)) на 2. Функция trunc() вычисляет целую часть выражения, указанного в качестве ее аргумента. В данном случае с помощью функции trunc() устанавливается, сколько целых полупериодов (T+t0) укладывается в интервале времени t. Если это число четное, то целочисленный остаток от его деления на 2 (значение переменной j) равен 0. В противном случае значение j равно 1.
Если j=0, то локальной переменной ТТ присваивается значение (T+t0)*frac(t/(T+t0)), т.е. переходим к локальному времени, равному остатку от вычитания из параметра процедуры t целого числа периодов (первое правило вычисления высоты и скорости шарика).
На заметку
Результатом выполнения функция frac() является дробная часть ее аргумента. Таким образом, результат команды frac(t/(T+t0)) – остаток от вычитания из t целого числа полупериодов, но только в отношении к интервалу времени (T+t0). Чтобы получить время в абсолютных единицах, данное число следует умножить на (T+t0).
Если же в интервале времени t вмещается нечетное число полупериодов (j=1), используем второе правило вычисления высоты и скорости шарика и присваиваем локальному параметру ТТ значение (T+t0) * (1-fгас (t/ (T+t0))).
После этого достаточно вычислить положение и скорость шарика в момент ТТ, который заведомо не превышает интервал (T+t0). Далее, если ТТ не превышает времени свободного падения шарика (t0), следует использовать формулу для свободного падения тела с высоты Н без начальной скорости. В противном случае зависимость высоты шарика от времени дается зависимостью Y(). Однако поскольку в послед-ией зависимости предполагается, что время отсчитывается от момента парения шарика на пружину, аргументом следует указать параметр (TT-t0), и то и сделано.
