Системы с колебаниями. Нахождение частоты малых колебаний маятника.
После инициализации переменной S в виде пустого списка, в этот список вносятся точки, формирующие пружину. Чтобы по базовым точкам сформировать пружину, используется процедура plot().
Теперь процедуру spring () используем для отображения двух соединенных друг с другом пружин. С этой целью определяем процедуру S(), параметрами которой являются высота фиксации пружин Н и угол alpha отклонения стержня, на котором подвешен шарик (этот угол нужен, чтобы определить длину каждой из пружин). Сформированные в процедуре графические объекты (левая и правая пружины) присваиваются в качестве значения локальным переменным S1 и S2 соответственно.
Левая пружина зафиксирована на левой стенке (горизонтальная координата равна 0) на высоте Н – это вертикальная координата. Если пружина расположена на высоте Н, расстояние между точкой подвеса стержня и точкой крепления пружины к стержню равно (1-Н) (в терминах задачи это параметр а). При отклонении стержня влево на угол alpha горизонтальная координата точки крепления пружины к стержню сместится в том же направлении на величину (1-H)*sin(alpha), и длина пружины будет равна 0.5-(1-H)*sin(alpha).
На заметку
Поскольку в условии задачи сказано, что шарик на стержне совершает малые колебания, можем полагать, что при отклонении стержня от вертикального положения обе пружины сжимаются вдоль горизонтальной линии Однако следует помнить, что это приближение, и оно справедливо только при незначительных отклонениях стержня.
Что касается правой пружины, то здесь нужно учесть следующее. Согласно определению процедуры spring(), ее параметром указывается левая точка пружины. Поэтому для правой пружины точкой фиксации является точка крепления ее к стержню – и эта точка совпадает с точкой крепления со стержнем левой пружины, т.е. это точка [0.5-(l-H)*sin(alpha),H]. Длина же правой пружины увеличивается на величину, на которую уменьшается длина левой пружины. Эта величина равна 0.5+(1-H)*sin(alpha).
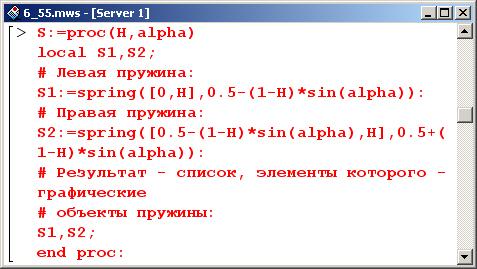
Результат выполнения процедуры S() формируется в виде последовательности.
Наконец, создаем процедуру Picture() для формирования всей картинки. У этой процедуры будет всего один аргумент – угол alpha отклонения стержня (влево). Высота крепления пружин и длина стержня определяются локальными переменными Н и L соответственно.
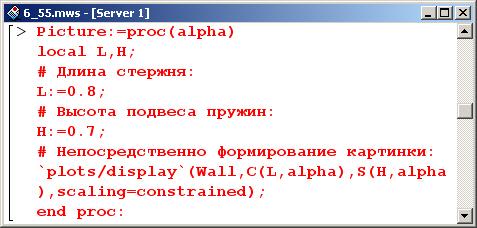
Картинка формируется процедурой 'plots/display'() с перечислением всех отображаемых объектов: трех стенок (переменная Wall), стержня и шарика (формируются командой С(L,alpha)), а также двух пружин (команда S(H,alpha)). Кроме того, чтобы масштабы по горизонтали и вертикали совпадали, указано значение опции scaling=constrained.
Теперь можно посмотреть, как система выглядит в состоянии равновесия (когда угол отклонения стержня равен 0).
После этого приступаем непосредственно к решению задачи. Заметим, что, поскольку в системе не действуют диссипативные силы, полная энергия системы не меняется. Полная энергия системы состоит из:
- а) кинетической энергии шарика;
- б) потенциальной энергии деформации пружин;
- в) потенциальной энергии шарика в гравитационном поле.