Системы с колебаниями. Нахождение частоты малых колебаний маятника.
Начнем с кинетической энергии, которая определяется через модуль скорости шарика. Его скорость, очевидно, направлена по касательной к описываемой шариком траектории (дуга окружности) и определяется через производную по времени от угла отклонения.
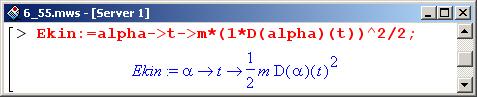
Энергию системы определим как оператор. В частности, оператор кинетической энергии шарика, зависящий от функции alpha (эта функция задает эволюцию системы во времени), действует на параметр t следующим образом.
Внимание!
В приведенном выше описании конструкция Ekin: = alpha › означает, что оператору Ekin в зависимости от параметра alpha ставится в соответствие то, что находится после стрелки (›). После стрелки находится код t › m*(l*D(alpha)(t))A2/2, определяющий действие Ekin на аргумент t. Таким образом показано, что оператору Ekin в соответствие ставится действие (поэтому Ekin и является оператором).
Практически так же определяется потенциальная энергия сжатой и разжатой пружин.
На заметку
Если пружина сжимается или разжимается на величину д:, то потенциальная энергия деформации пружины равна Е = кх 2/2, где к – жесткость пружины. Если расстояние от точки подвеса стержня до точки крепления пружины равно а, а стержень отклонился на угол а, то при малых углах отклонения можем полагать, что сжатие одной пружины и, разумеется, растяжение другой одинаковы и равны х = аа(t). Поскольку пружин две и каждая дает свой вклад в энергию деформации, полная энергия деформации пружин равна Е = ка2а2. Что касается потенциальной энергии шарика в поле силы тяжести, определяемой ниже, то удобно нулевой уровень для такой энергии выбрать на высоте, где шарик и стержень находятся в равновесии. Тогда при отклонении на угол а стержня шарик поднимется, по сравнению с первоначальным положением, на величину h*l(\-cos(a)) и его потенциальная энергия будет равна Е = mgl(\-cos(a(/))).
Прирост потенциальной энергии шарика в гравитационном поле при отклонении стержня от вертикали дается следующей зависимостью.
Полная энергия системы является суммой кинетической энергии, энергии деформации пружин и потенциальной энергии шарика в поле силы тяжести.
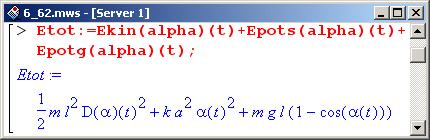
Следует заметить, что полная энергия Etot определена как переменная, а не как оператор.
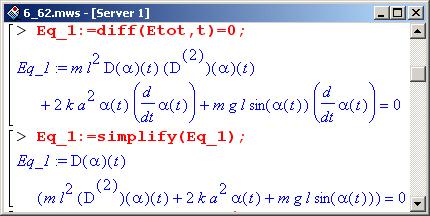
Как уже отмечалось, полная энергия системы (переменная Etot) при эволюции последней не меняется. Это значит, что если продифференцировать выражение для полной энергии по времени, то эта производная с неизбежностью должна равняться нулю. Таким образом, получаем уравнение движения.
