Гладкие кривые
Все умные места кривые.
Мераб Мамардашвшш
Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость. Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания как гладкого сопряжения, так и изгибов, например острых углов.
Прекрасным примером такого сочетания гладких кривых и острых преломлений являются профили авиакрыла. Обсудим гладкость кривых.
Пример-метафора
Продолжая метафору частицы, перемещающейся по кривой, можно сказать, что у нее на пути вдоль параметрической кривой не должно быть остановок (кроме начала и конца) и внезапного изменения направления.
Для того чтобы представить направление движения частицы, можно мысленно "укрепить" на ней стрелку, которая непрерывно указывает направление движения вдоль параметрической кривой.
На математическом языке стрелка на частице называется касательной. Если касательная в соседних точках не меняет внезапно своего направления, такую кривую считают гладкой (рис. 12.4).
Если "на кривой имеется излом, то направление касательной в точке Q меняется практически мгновенно (рис. 12.5).
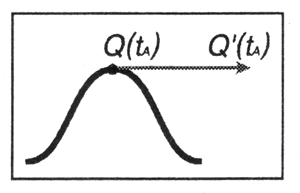
Рис. 12.4. Касательная на гладкой кривой
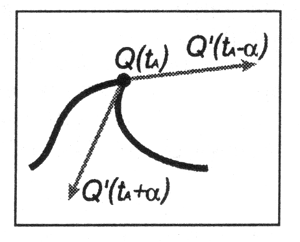
Рис. 12.5. Касательная на кривой с изломом
Теперь мы должны подробнее познакомиться с основами построения гладких кривых, применяющихся в векторной компьютерной графике. Начнем с NURBS-кривых, которые являются более общим (а соответственно, и более сложным) случаем таких кривых.
