Изменение формы кривой. Соединение нескольких секторов.
Как же изменить форму канонической кривой Безье, чтобы с ее помощью получить огромное многообразие форм, из которых можно составить объект любой сложности?
В программах векторной графики существует единственный способ – это интерактивное перемещение опорных и управляющих точек. Если перемещаются начальная или конечная точки, то кривая станет соответствующим образом изменяться (вытягиваться или сжиматься как упругая резинка). Перемещение управляющих точек изменяет кривизну соответствующей "половинки" кривой Безье, входящей в начальную или конечную точки (рис. 12.28).
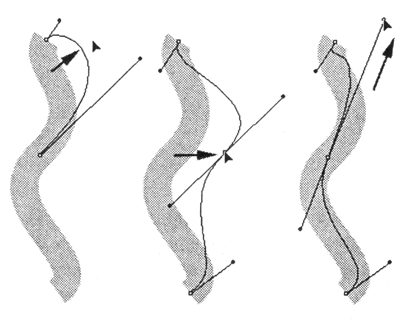
Рис. 12.28. Способы изменения формы сегмента
Таким образом, с помощью перемещения этих четырех точек получают неограниченное количество форм кривой Безье, которая может быть всего-навсего одним отдельным сегментом сложного секторного контура.
Разумеется, векторные редакторы позволяют работать одновременно с несколькими опорными точками (перемещать, вращать и т. п.).
Соединение нескольких секторов
Теперь необходимо рассмотреть, как создается многообразие контуров с помощью соединения нескольких канонических кривых Безье в связанную последовательность, часто даже замкнутую (рис. 12.29).
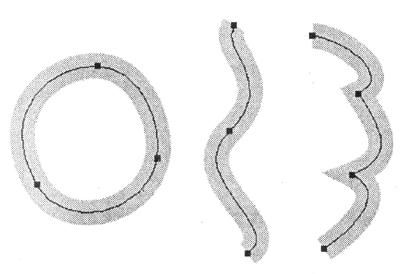
Рис. 12.29. Примеры векторных контуров, составленных из кривых Безье
В каждом сегменте можно добавлять опорные точки, в данном случае появляются две дополнительные управляющие точки с управляющими линиями, которые тоже позволяют изменять форму кривой. Добавление новых опорных точек в пределах одного сегмента кривой не противоречит тому условию, что отдельные кривые соединяются в цепь. Просто кривая Безье добавляется не к концу контура, а размещается внутри уже имеющегося контура.
Замечание
Для того чтобы отличать кривую как элементарную кривую, исходную кривую и кривую, которая уже находится в составе контура, последнюю чаще всего принято называть сегментом (сегментом контура или сегментом кривой).
По сути дела любая векторная конструкция (векторный контур или векторная форма) создается из векторных сегментов, каждый из которых идентичен отдельной элементарной кривой Безье.
Отсюда следует, что между ними образуются соединительные точки, которые иногда называются узлами (например, nodes – в графическом редакторе CorelDRAW). Метафора в этом случае очевидна: куски проволоки связываются узелками.
В других программах эти точки называются опорные точки (anchor point), дословно "якорные точки" (Adobe Illustrator), или просто точки (Macromedia FreeHand).
Для поддержки соотношения между элементарными сегментами существуют разные типы опорных точек.