Узлы. Характеристика семейства базовых функций.
На рис. 12.10 все базовые функции имеют одинаковую форму и размещены на равных расстояниях друг от друга. Это очень симметрично и элегантно, но на самом деле желательно варьировать длины интервалов таким образом, чтобы определенные контрольные точки влияли на значительно больший сегмент кривой, а определенные – на меньший. Это создает условие для неоднородности (Non-Uniform) в описании кривой.
Однако определение последовательности точек, на которые разбивается ось параметра t, является не очень легкой задачей. Ведь при изменении относительных интервалов между такими точками, вам представится возможность менять длительность воздействия контрольных точек на движущуюся вдоль кривой частицу.
Точки, разграничивающие интервалы, получили название узлов (knots), а их упорядоченный список – название узлового вектора (knot vector).
Узловой вектор базовой функции, представленный на рис. 12.11, имеет вид:
{0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}Это пример однородного узлового вектора (uniform knot vector), в котором все функции определены на одинаковых временных интервалах.
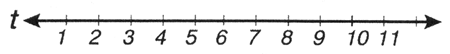
Рис. 12.11. Пример однородного узлового вектора
Следующий рисунок (рис. 12.12) представляет пример кривой, созданной на основе такого узлового вектора.
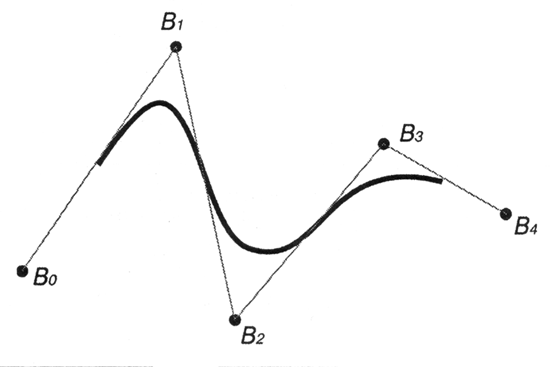
Рис. 12.12. NURBS-кривая с однородным узловым вектором
Если изменить узловой вектор, например, следующим образом:
{0.0, 1.0, 2.0, 3.75, 4.0, 4.25, 6.0, 7.0}…то получится другое множество неоднородных (non-uniform) базовых функций (рис. 12.13) и, соответственно, другая форма кривой (рис. 12.14), которая строится на тех же контрольных точках, что и на рис. 12.12.
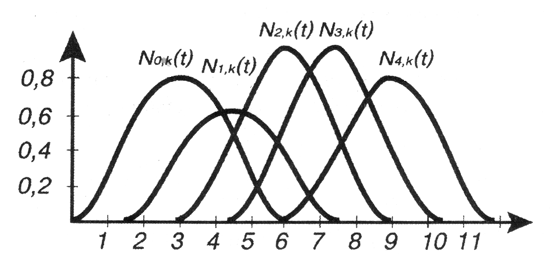
Рис. 12.13. Неоднородные базовые функции для множества контрольных точек
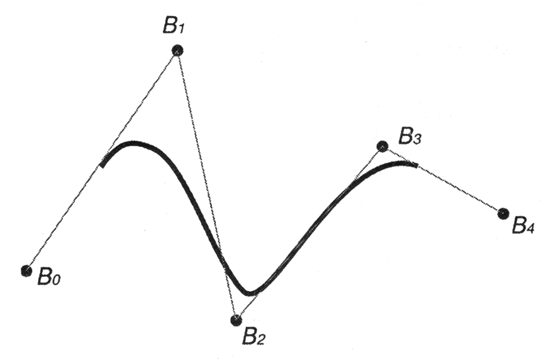
Рис. 12.14. NURBS-кривая с неоднородным узловым вектором
Характеристика семейства базовых функций
Для любого значения параметра t сумма всех базовых функций строго равна 1.
Если веса всех контрольных точек положительны, кривая лежит в области, полученной соединением крайних (внешних) контрольных точек. Такой "габаритный" контейнер получил название "выпуклой оболочки" (convex hull).
