Рациональные кривые
Обратимся к ключевой букве в названии NURBS – "R", что означает "rational" (рациональный). Рациональные кривые, в сравнении с обычными (нерациональными – "non-rational") В-сплайнами, обладают двумя дополнительными и очень важными свойствами:
- они обеспечивают корректный результат при проекционных трансформациях (например, масштабировании), а нерациональные В-сплайны – только при аффинных трансформациях (например, перемещениях);
- их можно использовать для моделирования кривых любого вида, включая конические сечения (окружности, эллипсы, параболы и гиперболы).
Эти свойства (кстати, весьма значительные) достигаются за счет четырехмерного представления обычной трехмерной контрольной точки {х, у, z}. Это значит, что каждая контрольная точка представляется четырьмя координатами {х, у, z, w}. Последняя координата w означает вес (weight) контрольной точки, о котором уже упоминалось ранее (вспомним пример с гравитацией или холодильником).
Замечание
"Вес" в математическом смысле – это значение, важность, влияние, которое выражается особой функцией или числовым значением. Это одно из важных понятий в теории принятия решений.
Изначально координата w равняется единице, но при увеличении этого значения для контрольной точки увеличивается степень ее воздействия на форму кривой и последняя сильнее выгибается в сторону контрольной точки (рис. 12.15).
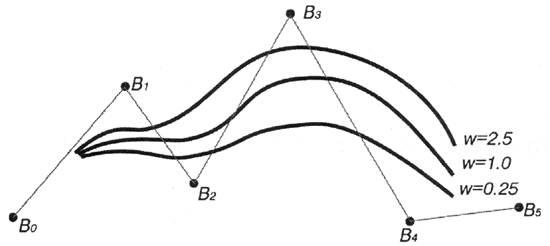
Рис. 12.15. Изменение формы кривой при изменении веса контрольной точки
Замечание
Важно заметить, что существенным является только относительное изменение весов контрольных точек. Если вдвое увеличить веса всех контрольных точек, то форма кривой не изменится.
Пример
Квадратичная (второй степени) NURBS-кривая определяется тремя контрольными точками (рис. 12.16). У всех трех кривых узловой вектор имеет вид:
{0.0, 0.0, 0.0, 1.0, 1.0, 1.0}Веса первой и последней контрольных точек у каждой кривой равны 1. Если вес центральной вершины меньше 1, то результирующая кривая представляет собой сегмент эллипса (рис. 12.16, а). Если ее вес равняется 1, образуется парабола (рис. 12.16, б). Если же ее вес гораздо больше 1, то кривая преобразуется в гиперболу (рис. 12.16, в).
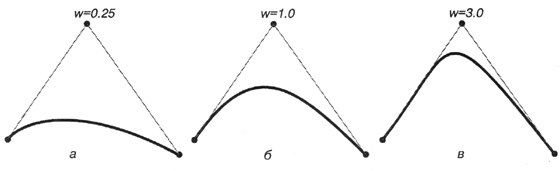
Рис. 12.16. NURBS-кривые с различными весами центральной контрольной точки
При всех своих непревзойденных свойствах NURBS-кривые все же обладают следующим громадным недостатком: расширенные возможности не могли не сказаться на уровне и сложности инструментария для их построения, а это, в свою очередь, требует от дизайнера повышенных условий для освоения, не говоря уже о необходимости определенного уровня математической подготовки (иначе трудно ожидать, что удастся разобраться во всех преимуществах и получить творческую свободу).
