Геометрические объекты
Весьма проблематично в кратком обзоре возможностей трехмерной графики исчерпывающе рассказать обо всем многообразии инструментов моделирования, используемых в различных программах. Поэтому оставляем за собой право выбрать один из самых распространенных и мощных ЗВ-пакетов и на его примере обсудить основные типы объектов и технологии их моделирования. В качестве референтной программы ЗВ-моделирования и анимации был выбран уже упоминаемый пакет 3D Studio MAX компании Discreet.
Вот краткий перечень типов геометрических объектов, которые могут быть созданы в этой программе.
Сплайновые кривые (spline curves) (рис. 13.4) – это смоделированные таким образом кривые (Безье или NURBS), что они могут служить заготовками для построения поверхностей (экструзии, тела вращения или лофтинга) или их можно использовать в качестве траектории движения. Для кривых Безье определен, в частности, набор примитивов (например, окружность или текст), которые впоследствии могут быть конвертированы в явное ("повершинное") описание формы. При отображении на экране и при финальной визуализации кривые аппроксимируются линейными отрезками с заданной точностью.
Рис. 13.4. Онлайновые кривые
Полигональные объекты (polygonal objects) (рис. 13.5) – это полигональные примитивы (polygonal primitives), описываемые наборами динамически изменяемых параметров (например, длин, радиусов) или полигональные сетки (polygonal meshes), определяемые как наборы граней (faces), ограниченных ребрами (edges), попарно соединяющими вершины (vertices). Использование примитивов резко облегчает дизайнеру (и программе!) манипулирование формой объекта, однако служит определенным ограничением при построении сложных полигональных поверхностей. При визуализации таких 3D-примитивов (например, сфер или цилиндров) их форма аппроксимируется гранями с заданной точностью (речь идет о так называемой "сегментации"). Так как поверхность полигонального объекта представляет собой, в конечном счете, набор плоских граней, то для придания ей визуальной гладкости применяют различные алгоритмы сглаживания (smoothing). В виду относительно малой затратности вычислительных ресурсов компьютера при интерактивной визуализации таких объектов данная технология моделирования широко используется при создании 3D-игр и виртуальных миров.
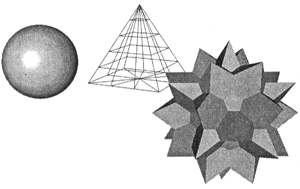
Рис. 13.5. Полигональные объекты
Поверхности Безье (Bezier patches) (рис. 13.6) – это математически гладкие поверхности, описываемые расположением вершин Безье. Эти вершины определяют их кривизну при помощи дополнительных управляющих точек (control points) на концах касательных к поверхности векторов (tangent vectors). Подобные поверхности требуют большей нагрузки для вычислительной системы, зато позволяют моделировать сложные криволинейные (например, даже органические) формы объектов.
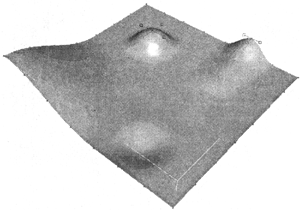
Рис. 13.6. Поверхность Безье
NURBS-поверхности (Non-Uniform Rational B-splines surfaces) (рис. 13.7) – это наиболее универсальный и эффективный способ моделирования неоднородных криволинейных поверхностей. Такие поверхности описываются в особом четырехмерном гомогенном (однородном) пространстве (homogeneous space), в котором каждая управляющая вершина (control vertex), кроме трех координат х, у и z, имеет еще и дополнительную весовую (weight) характеристику. Изменяя положение и относительный вес вершины, можно предельно точно управлять формой объекта.
Рис. 13.7. NURBS-поверхность