Мера расстояния и мера сходства
Два следующих примера помогут нам разобраться в особенностях работы с мерами расстояния.
Пример первый: сходства между дихотомическими переменными
- Создайте сначала таблицу сопряженности для переменных item3 и item 14. Эти переменные соответствуют ответам на вопросы "Считаете ли Вы, что развитие космонавтики необходимо?" и соответственно "Согласились бы Вы предоставить себя в распоряжение ученым для научных экспериментов?" (с кодировками 1 = да и 2 = нет).
Частоты в таблице 2x2 распределились следующим образом:
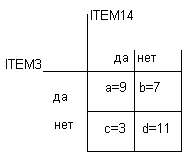
Рис. 15.5: Частоты в таблице 2x2
- Выберите в меню Analyze… (Анализ) › Correlate… (Корреляция) › Distances… (Расстояния)
- Перенесите переменные item3 и item 14 в поле тестируемых переменных.
- Активируйте расчет расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities… (Подобия).
- Щелкните на кнопке Measures… (Меры) и, в открывшемся диалоговом окне, активируйте Binary (Бинарные). Оставьте предварительную установку мер вычисления по методу Рассела и Рао.
- Так как в приведенном примере отрицательному ответу присвоен код 2, а в предварительных установках предусмотрен 0, то Вам необходимо откорректировать это значение в поле Absent (Отсутствует).
- Покиньте диалоговое окно мер нажатием Continue (Далее) и в главном диалоговом окне начните расчет щелчком на ОК.
В результате Вы получите значение меры подобия равное 0.3. Оно определяется как частное от деления частоты а на сумму всех четырех частот:
Proximity Matrix (Матрица близости)
| Russell and Rao Measure (Мера подобия Рассела и Рао) | ||
| ITEM3 | ITEM14 | |
| ITEM3 ITEM 14 |
0.300 | 0.300 |
- This is a similarity matrix (Это матрица подобия).
Пример второй: расчет корреляционной матрицы 2x2 в качестве базиса для факторного анализа
Мы хотим рассчитать корреляционную матрицу для восемнадцати переменных item1-item18 с применением четырехточечная корреляция фи. В этом случае корреляционную матрицу можно использовать в качестве базиса для факторного анализа. Для решения этой задачи нам предстоит поработать с программным синтаксисом SPSS.
- Перенесите переменные item1-item18 в поле тестируемых переменных.
- Активируйте расчет расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities… (Подобия).
- Откройте щелчком на кнопке Measures… (Меры) соответствующее диалоговое окно, активируйте в нем Binary (Бинарные) и присвойте параметру Absent (Отсутствует) код 2. В заключении вместо меры по Расселу и Рао выберите 4 точечную µ-корреляцию.
- При помощи щелчка на Continue (Далее) вернитесь в основное диалоговое окно, после прохождения кнопки Paste… (Вставить) просмотрите синтаксис команд.
- Внесите в синтаксис следующие корректировки:
PROXIMITIES item1 item2 item3 item4 item5 item6 item7 item8 item9 item10 item11 item12 Lzem13 item14 item15 item16 item17 item18VIEW = VARIABLE MEASURE = PHI(1.2) MATRIX = OUT(*) SSCODE rowtype_("PROX" = 'CORR') FACTOR / MATRIX = IN(COR = *)- Начните расчет при помощи символа Syntax-Start (Синтаксис-Начать).
В окне просмотра появятся результаты факторного анализа, а в окне редактора данных будет показана корреляционная матрица.
