Расчет уравнения регрессии
Откройте файл hyper.sav.
- Выберите в меню Analyze… (Анализ) › Regression… (Регрессия) › Linear… (Линейная) Появится диалоговое окно Linear Regression (Линейная регрессия).
- Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.
- Ничего больше не меняя, начните расчет нажатием ОК.
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
| Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Смещенный R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
| 1 | 0.861а | 0.741 | 0.740 | 25.26 |
- а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
ANOVAb
| Model (Модель) | Sum of Squares (Сумма Квадратов) | df | Mean Square (Среднее значение квадрата) | F | Sig. (Значимость) | |
| 1 | Regression (Регрессия) | 314337.948 | 1 | 314337.9 | 492.722 | 0.000a |
| Residual (Остатки) | 109729.408 | 172 | 637.962 | |||
| Total (Сумма) | 424067.356 | 173 |
- a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина)
- b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
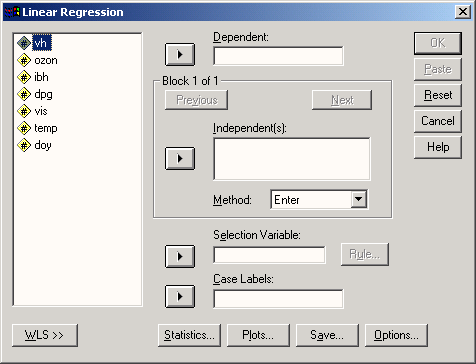
Рис.16.2: Диалоговое окно Линейная регрессия
Coefficients (Коэффициенты)а
| Model (Модель) | Unstandardized Coefficients (Не стандартизированные коэффициенты) | Standardized Coefficients (Стандартизированные коэффициенты) | Т | Sig. (Значимость) | |||
| В | Std. Error (Стандартная ошибка) | ß (Beta) | |||||
| 1 | (Constant) (Константа) | 34.546 | 9.416 | 3.669 | 0.000 | ||
| Cholesterin, Ausgangswert (холестерин, исходная величина) | 0.863 | 0.039 | 0.861 | 22.197 | 0.000 | ||
- a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчетов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем "константа". То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0.863 - chol0 + 34.546Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента (3 будет рассмотрено при изучении многомерного анализа.
Средняя часть расчетов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется "коэффициентом детерминации". В таблице результатов это частное выводится под именем "R-квадрат". В нашем примере мера определенности равна:
314337.948 / 424067.356 = 0.741Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определенности всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэффициента детерминации, обозначаемый "R", равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэффициент детерминации. Величина "смещенный R-квадрат" всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определенности корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии. О том, как регрессионную прямую можно встроить в диаграмму рассеяния, будет рассказано в разделе 16.1.3.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots…(Графики) зайдете в соответствующее диалоговое окно и зададите в нем параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.