Нелинейная регрессия
Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду. Один пример линейной связи из области медицины был приведен в главе 16.1; еще одним, уже знакомым нам примером является линейная связь между весом и ростом. При условии наличия лопаточного количества респондентов, на основании измеренных пар значений можно вывести уравнение регрессионной прямой, к которой более или менее приближается количество точек, соответствующие парам значений.
Существуют также линейные связи, следующие непосредственно из физических закономерностей. Так путь s, пройденный, при постоянной скорости с за промежуток времени: рассчитывается по формуле:
s = c * tСтало быть, путь является линейной функцией времени. А если мы рассмотрим закон свободного падения, то в этом случае расстояние s. которое проходили падающее тело увеличивается пропорционально квадрату времени:
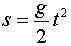
Где g – ускорение свободного падения.
Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряженном, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
| s (см) | t (сек) |
| 5 | 1.0 |
| 9 | 1.4 |
| 16 | 1.8 |
| 26 | 2.3 |
| 40 | 2.8 |
| 65 | 3.6 |
| 98 | 4.5 |
Хотя связь между 5 и с и не является линейной, ее можно перевести в линейную модель, если взять квадратный корень из обоих сторон закона свободного падения:
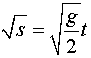
С помощью преобразования данных, мы разрешаем компьютеру создать новую переменную, содержащую значения квадратного корня из величины s и рассматривать ее как зависимую переменную, а время / как независимую переменную. Рассчитаем коэффициент регрессии b так, как это было изложено в разделе 16.1.
Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
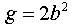
Если Вы выполните эти вычисления, то получите b = 0.2224 и g = 9.88.
При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь у = аеbx можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения:
ln(y) = ln(a) + bxТо есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регрессии вычисляются непосредственно, а не определяются с помощью итераций.
