Нелинейная регрессия
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
| Год | Лекала | Население |
| 1790 | 0 | 3.895 |
| 1800 | 1 | 5.267 |
| 1810 | 2 | 7.182 |
| 1820 | 3 | 9.566 |
| 1830 | 4 | 12.834 |
| 1840 | 5 | 16.985 |
| 1850 | 6 | 23.069 |
| 1860 | 7 | 31.278 |
| 1870 | 8 | 38.416 |
| 1880 | 9 | 49.924 |
| 1890 | 10 | 62.692 |
| 1900 | 11 | 75.734 |
| 1910 | 12 | 91.812 |
| 1920 | 13 | 109.806 |
| 1930 | 14 | 122.775 |
| 1940 | 15 | 131.669 |
| 1950 | 16 | 150.697 |
| 1960 | 17 | 178.464 |
В таблице приведена численность населения в миллионах и дополнительно количество декад (десятилетий), прошедших с 1790 года.
Зависимость численности населения (переменная pop) от времени t (выраженного здесь в декадах) часто описывается при помощи следующей формулы:
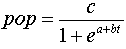
Эту связь нельзя перевести в линейную форму. Она включает три параметра: а, b и с, которые должны быть определены при помощи подходящего метода. Для этого необходимо задать начальные значения этих параметров.
Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3.895 = 200/(1+e2)
И следовательно:
a = ln(200 / 3.895 - 1) = 3.9Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра b:
5.267=200/(1+e3.9+b)
И следовательно:
b = ln(5.267 - 1) - 3.9 = -0.3Определим теперь более точные значения параметров а, b и с с помощью итераций.
- Откройте файл usa.sav.
- Выберите в меню Analyze… (Анализ) › Regression… (Регрессия) › Nonlinear… (Нелинейная)
- В диалоговом окне Nonlinear Regression (Нелинейная регрессия) перенесите переменную pop в поле для зависимых переменных.
- Щелкните на поле Model Expression (Модельное выражение) и внесите в него следующую формулу:
c / (1 + exp(a + b * dekade))