Нелинейная регрессия
При вводе формулы можно использовать клавиатуру, находящуюся в диалоговом окне. Диалоговое окно будет выглядеть так, как изображено на рисунке 16.15. Нам осталось только задать начальные значения параметров.
- Щелкните на кнопке Parameter… (Параметр)
Вы получите диалоговое окно, в котором сможете задавать начальные значения.
- Укажите в поле имен имя первого параметра, то есть, к примеру, а, затем щелкните в поле Starting value (Начальное значение), введите значение 3.9 и щелкните на Add (Добавить).
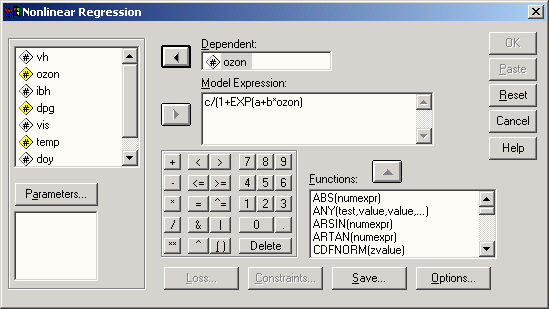
Рис. 16.15: Диалоговое окно Nonlinear Regression (Нелинейная регрессия).
- Поступите таким же образом с двумя другими параметрами бис (начальные значения -0.3 и 200 соответственно).
- Покиньте диалоговое окно нажатием Далее.
- Щелкните на кнопке Save (Сохранить). Отметьте в диалоговом окне Nonlinear Regression: Save New Variables (Нелинейная регрессия: Сохранить новые переменные) параметры: Predicted Values (Прогнозируемые значения) и Residuals (Остатки). Таким образом, Вы создадите две новые переменные (с именами: pred_ и resid), которые содержат вычисленные значения и остатки для каждого года.
- Начните расчет нажатием ОК.
На экране появятся результаты, причем Вы можете заметить, что вывод происходит не в виде привычных современных таблиц. Сначала протоколируется процесс итерации; в рассматриваемом примере для достижения заданного уровня точности понадобилось 10 итерационных шагов. Дополнительно выводятся следующие статистические характеристики:
| Nonlinear Regression | Summary Statistics Dependent Variable POP | ||
| Source | DF | Sum of Squares | Mean Square |
| Regression | 3 | 123048.61437 | 41016.20479 |
| Residual | 15 | 186.50337 | 12.43356 |
| Uncorrected Total | 18 | 123235.11774 | |
| (Corrected Total) | 17 | 53291.50763 | |
| R squared = 1Residual SS / CorrectedSS =, 99650 | |||
Здесь интерес может представлять только член, обозначенный R squared; его следует понимать как часть суммарной дисперсии, которая обусловлена построенной моделью. Вычисленное значение этого параметра, 0.9965, указывает на очень хорошую степень приближения. После этого вывода следует распечатка конечных значений всех трех параметров вместе с соответствующей стандартной ошибкой и доверительным интервалом:
| Asymptotic 95% Asymptotic Confidence Interval | ||||
| Parameter Estimate | Std. Error | Lower Upper | ||
| A | 3.888771432 | 093688592 | 3.6890789254 | 0.088463938 |
| В | -0.278834486 | 015593535 | -0.312071318 | -0.245597654 |
| С | 244.01372955 | 17.974966354 | 205.70099568282 | 0.32646341 |
Завершает список выводимых результатов корреляционная матрица оценок параметров:
| Asymptotic | Correlation А | Matrix of В | the | Parameter Estimates С |
| А | 1.0000 | -0.724 | 3 | -0.3759 |
| В | -0.7243 | 1.000 | 0.0 | 0.9043 |
| С | -0.3759 | 0.904 | 3 | 1.0000 |
Очень высокие абсолютные значения корреляций указывают на то, что модель содержит неоправданно большое количество параметров. В рассматриваемом примере и модель с меньшим количеством параметров даст столь же хорошее приближение.
- Если Вы хотите визуально сравнить рассчитанные значения с наблюдаемыми, то можете посредством меню Graph… (Графики) › Scatter plots… (Диаграммы рассеяния) построить многослойную диаграмму рассеяния (Staggered), на которой Вы можете представить переменные pop и pred_ в зависимости от переменной jahr. Также можно поступить и с остатками (переменная rcsid).
Согласно предварительным установкам при расчете нелинейной регрессии происходит минимизация суммы квадратов остатков. При помощи кнопки Loss…(Остаток) можно задать какую-либо другую минимизирующую функцию. Далее при помощи кнопки Constraints…(ограничения) может быть открыто окно, в котором можно задать ограничения для определяемых параметров нелинейной регрессии.
