Бинарная логистическая регрессия
Качество приближения регрессионной модели оценивается при помощи функции подобия. Мерой правдоподобия служит отрицательное удвоенное значение логарифма этой функции (-2LL). В качестве начального значения для -2LL применяется значение, которое получается для регрессионной модели, содержащей только константы. После добавления переменной влияния tzell значение -2LL равно 43.394; это значение на 18.789 меньше, чем начальное. Подобное снижение величины означает улучшение; разность обозначается как величина хи-квадрат и является очень значимой.
Это означает, что начальная модель после добавления переменной tzell претерпела значительное улучшение. Если при наличии некоторого количества независимых переменных анализ производится не при помощи метода вложения, а пошаговым образом, то получающиеся изменения отображаются в разделах "Блок" и "Шаг". При этом, если Вы производили ввод переменных в блочной форме, то показатель в разделе "Блок" приобретает особое значение.
Два других выведенных показателя, названные именами Кокса & Шела и Наделькеркеса, являются мерами определенности. Они также как и при линейной регрессии указывают на ту часть дисперсии, которую можно объяснить с помощью логистической регрессии. Мера определенности по Коксу и Шелу имеет тот недостаток, что значение равное 1 является теоретически не достижимым; этот недостаток устранен благодаря модификации данной меры по методу Наделькеркеса. Часть дисперсии, объяснимой с помощью логистической регрессии, в данном примере составляет 45.6%.
Далее приводится классификационная таблица, в которой наблюдаемые показатели принадлежности к группе (1 = болен, 2 = здоров) противопоставляются предсказанным на основе рассчитанной модели.
Classification Table (Классификационная таблица)а
| Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
| GRUPPE (Группа) | Percentage Correct (Процентный показатель верных показателей) | ||||
| Krank (болен) | Gesund (здоров) | ||||
| Шаг 1 | GRUPPE (Группа) | Krank (болен) | 18 | 6 | 75.0 |
| Gesund (здоров) | 4 | 17 | 81.0 | ||
| Overall Percentage (Суммарный процентный показатель) | 77.8 | ||||
- a. The cut value is 0.500 (Разделительное значение равно 0.500)
Из таблицы можно сделать вывод о том, что из общего числа больных, равного 24, тестом были признаны таковыми только 18 (в медицинской диагностике в таких случаях говорят о "строго положительных" результатах). Остальных 6 называют "ложно отрицательными"; они были признаны тестом здоровыми, хотя и являются больными. Из общего числа здоровых, равного 21, тестом были признаны таковыми только 17 ("строго отрицательные"), 4 признаны больными, хотя они и являются здоровыми ("ложно положительные"). В общем, правильно были распознаны 35 случаев из 45, это составляет 77.8%.
В заключении выводятся результаты о рассчитанных коэффициентах и проверке их значимости:
Variables in the Equation (Переменные в уравнении)
| В (Коэффициент регрессии В) | S.E. (Стандартная ошибка) | Wald (Вальд) | df | Sig. (Значимость) | Ехр (В) | ||
| Step 1 (Шаг 1) | TZELL | 0.278 | 0.082 | 11.599 | 1 | 0.001 | 1.321 |
| Constant (Константа) | -19.005 | 5.587 | 11.571 | 1 | 0.001 | 0.000 | |
- a. Variable(s) entered on step 1: TZELL (Переменные, введенные на шаге 1: TZELL)
Проверка значимости отличия коэффициентов от нуля, проводится при помощи статистики Вальда, использующей распределение хи-квадрат, которая представляет собой квадрат отношения соответствующего коэффициента к его стандартной ошибке.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В приведенном примере получились сверх значимые коэффициенты а = -19.005 bt = 0.278. При помощи этих двух значений коэффициентов мы можем для каждого значения Т-типизации рассчитать вероятность р. К примеру, для некоего обследуемого со значением Т-типизации 72 получим:
z = -19.005 + 0.278 * 72 = 1.018И таким образом:
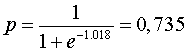
Рассчитанная вероятность р всегда указывает на исполнение предсказании, которое соответствует большей из двух кодировок зависимых переменных, в данном случае – на исполнение предсказания "здоров". Следовательно, рассматриваемый человек является здоровым с вероятностью 0.735.
