Множественная линейная регрессия
Вдобавок ко всему для каждого шага анализируются исключенные переменные. В вышеприведенной таблице в объяснениях нуждаются лишь коэффициенты ß. Это – регрессионные коэффициенты, стандартизованные соответствующей области значений, они указывают на важность независимых переменных, вовлеченных в регрессионное уравнение.
Уравнение регрессии для прогнозирования значения CPITN выглядит следующим образом:
cpitn = 0.032 * Alter - 0.379 * pu + 0.229 * zb - 0.083 * s + 0.143 - benif2 + 2.022Для 40-летнего рабочего с неполным школьным образованием, который ежедневно чистит зубы один раз в день и меняет щетку раз в полгода, с учетом соответствующих кодировок, получается следующее уравнение:
cpitn = 0.032 * 40 - 0.379 * 2 + 0.229 * 3 - 0.083 * 2 + 0.143 * 1 + 2.022 = 3.208При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков, на которых мы здесь останавливаться не будем. Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически) и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts… (Диаграммы) построить гистограмму остатков. В приведенном примере наблюдается довольно хорошее согласование гистограммы остатков с нормальным распределением.
Проверка на наличие систематических связей между остатками соседних случаев (что, однако, является уместным только при наличии так называемых данных с продольным сечением), может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию. Этот тест вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует. Тест Дарбина-Ватсона можно активировать через кнопку Statistics (Статистические характеристики). В данном примере тест дает удовлетворительное значение коэффициента, равное 1.776.
Еще одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule… (Правило) в диалоговом окне Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие, которое будет ограничивать количество случаев, вовлеченных в анализ.
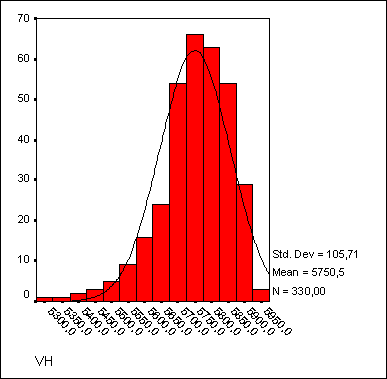
Рис. 16.14: Гистограмма остатков
