Корреляции
В этой главе речь пойдет о связи (корреляции) между двумя переменными. Расчеты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.
Если в качестве примера мы возьмем данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav), то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая; пара значений маркируется при помощи определенного символа. Такой график, называемый "диаграммой рассеяния" для двух зависимых переменных можно построить путем вызова меню Graphs… (Графики) › Scatter plots… (Диаграммы рассеяния) (см. гл. 22.8).
Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц. Это, конечно же, не является неожиданностью; данный пример был выбран, чтобы продемонстрировать наличие явной связи.
Статистик говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции. Этот коэффициент, всегда обозначаемый латинской буквой г, может принимать значения между -1 и +1, причем если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.
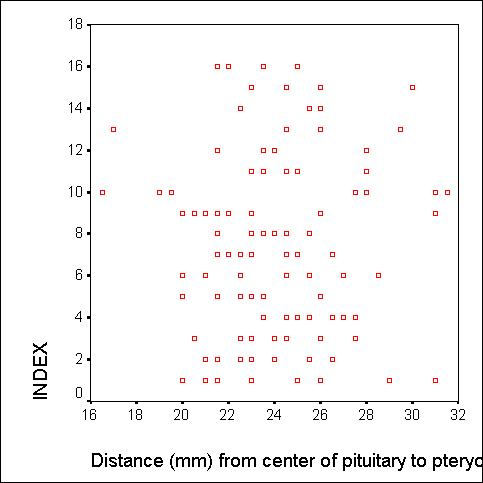
Рис. 15.1.Диаграммы рассеяния
Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следующие градации:
| Значение | Интерпретация |
| до 0.2 | Очень слабая корреляция |
| до 0.5 | Слабая корреляция |
| до 0.7 | Средняя корреляция |
| до 0.9 | Высокая корреляция |
| свыше 0.9 | Очень высокая корреляция |
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные.
- Переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений).
- По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределенной: ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.
- Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применен расчет ранговой корреляции.
- Обе переменные являются дихотомическими: четырехполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).
Расчет коэффициента корреляции между двумя недихотомическими переменными не лишен смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Еше один раздел специально посвящен частной корреляции.
