Отдельный тест по критерию хи-квадрат
Получилось очень значимое значение критерия хи-квадрат (р = 0.001). В рассматриваемом случае желателен вывод не абсолютных, а стандартизированных остатков, определяемых по формуле:
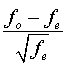
При помощи основополагающего правила, приведенного в главе 8.7.2, можно точно определить те категории, для которых наблюдается значительное отклонение наблюдаемых частот от ожидаемых.
Стандартизированные остатки >= 2.0 указывают на значительное, >= 2.6 на очень значительное и >= 3.3 на сверх значительное отклонение. Если следовать этому правилу, то в экспериментах с игральной костью наблюдается очень значимое превышение количества выпадений 3 очков и очень, очень значимое занижение количества выпадений 6 очков.
Во втором примере, который принадлежит к области ботаники, нужно проверить не равномерное распределение, а наличие распределения подчиняющегося заданному соотношению.
Потомки трех сортов бобовой культуры были разделены на три типа, которые находятся в соотношении между собой как 1:2:1. Во время некоторого эксперимента, проведенного с сотней таких потомков тип 1 появился 29 раз, тип 2-44 раза и тип 3-27 раз. Необходимо исследовать значительно ли отклоняется полученное распределение от теоретического распределения 1:2:1.
Данные находятся в файле bohnen.sav, причем переменная typ соответствует типу, а переменная n частоте.
- Откройте файл bohnen.sav.
- Сначала действуйте так же, как в первом примере, и взвесьте наблюдения с частотной переменной n.
- В диалоговом окне Chi-Square Test (тест Хи-квадрат) присвойте переменной typ статус тестируемой переменной.
- В поле Expected values (Ожидаемые значения) активируйте в этот раз опцию Values (Значения). Введите числа 1, 2 и 1 в предусмотренное для этого поле, и щелкните дополнительно на кнопке Add (Добавить).
- Запустите расчет путем нажатия ОК.
В окне просмотра появятся следующие результаты:
Тур (Тип)
| Observed N (Наблюдаемое N) | Expected N (Ожидаемое N) | Residual (Остаток) | |
| 1 | 29 | 25.0 | 4.0 |
| 2 | 44 | 50.0 | -6.0 |
| 3 | 27 | 25.0 | 2.0 |
| Total (Сумма) | 100 |
Test Statistics (Статистика теста)
| Тур (Тип) | |
| Chi-Square (Хи-квадрат) а | 1.520 |
| Of | 2 |
| Asymp. Sig. (Статистическая значимость) | 0.468 |
- а. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 25.0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 25.0.)
Ожидаемые частоты выстроены в соответствии с заданным соотношением. На сей раз значимого отклонения наблюдаемых частот от ожидаемых не наблюдается (р = 0.468).
