Задача вращения
Рассмотрим поподробнее задачу вращения. Используем для этого приводившийся в разделе 19.2 пример опроса, исследующего отношение к иностранцам.
- Откройте файл ausland.sav.
- Выберите в меню Analyze (Анализ) › Data Reduction (Сокращение объема данных) › Factor… (Факторный анализ)
- В диалоговом окне Factor Analysis (Факторный анализ) поместите переменные a1-а15 в поле тестируемых переменных.
- С помощью кнопки Extraction… (Извлечение) укажите требуемое число создаваемых факторов равное двум, чтобы получить легко интерпретируемый двумерный пример.
- Через выключатель Rotation… (Вращение) активируйте опцию Loading plot(s) (Диаграмма нагрузок), но для модели вращения оставьте установленную по умолчанию опцию None (Отсутствует).
- В результате мы оставляем вывод так называемой компонентной диаграммы.
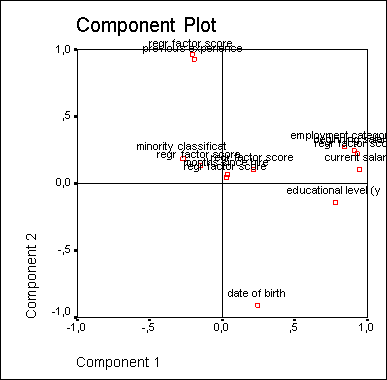
Рис. 19.8: Компонентная диаграмма без вращения
На этой диаграмме в графическом виде представлены факторные нагрузки обоих факторов. Для интерпретации факторов было бы оптимально, если бы точки лежали ближе к осям и подальше от точки начала отсчета; тогда каждая переменная имела бы значительную нагрузку для одного фактора и незначительную для другого. Этого можно достичь поворотом осей против часовой стрелки, причем ортогональность системы координат (прямой угол между осями) должна сохраниться. В данном двумерном примере это вращение можно представить себе довольно наглядно, математически же подобный поворот можно произвести также и в и-мерном пространстве (то есть при наличии произвольного количества факторов).
Альтернативой прямоугольному (ортогональному) вращению является косоугольное вращение. В этом случае после вращения оси не сохраняют прямой угол по отношению друг к другу. В то время как при прямоугольном вращении корреляция между факторами отсутствует, то при косоугольном вращении этот принцип нарушается – факторы могут коррелировать между собой.
SPSS предлагает в общей сложности пять методов вращения: три метода для ортогонального вращения, один для косоугольного и еще один, который является комбинацией двух видов вращения. Эти методы Вы можете активировать через выключатель Rotation… (Вращение) в диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение).
- Varimax: Ортогональное вращение, при котором происходит минимизация количества переменных с высокой факторной нагрузкой. Этот метод является наиболее часто применяемым, поскольку он облегчает интерпретацию факторов.
- Quartimax: Ортогональное вращение, при котором происходит минимизация количества факторов, необходимых для объяснения переменной. Этот метод используется редко и вообще не рекомендуется для применения.
- Equamax: Ортогональное вращение; компромисс между предыдущими методами.
- Direct oblimin: Косоугольное вращение.
- Рrоmах: Комбинация ортогонального и косоугольного видов вращений.
Обычно для ортогонального вращения применяют метод варимакса, а для косоугольного – Direct oblimin. При помощи компонентной диаграммы отследим действие вращения, осуществленного с использованием метода варимакса.
- В диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение) вместо опции None (Отсутствует) активируйте опцию Varimax (Baримакс).
- Рассмотрите измененную компонентную диаграмму.
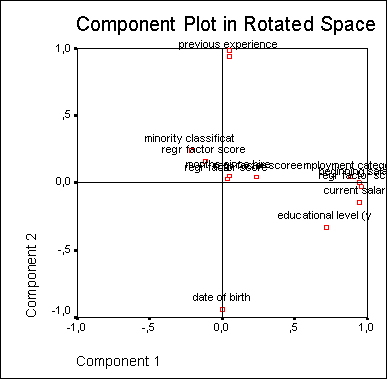
Рис. 19.9: Компонентная диаграмма после вращения
На диаграмме стало заметно смещение факторных нагрузок в сторону главных осей.
Факторный анализ является самым излюбленным приемом практических статистиков, служащим для сокращения количества переменных. Наиболее интересной частью факторного анализа является толкование получающихся факторов, над которым, правда, придется поразмыслить и применить весь имеющийся опыт.
