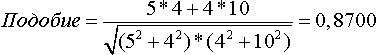Меры расстояния и меры сходства. Метрические переменные.
Основой кластеризации (образования групп) наблюдений является дистанционная матрица и матрица подобия наблюдений. Так как расстояние (дистанция) также применяется и для оценки подобия, то разница между этими двумя матрицами не велика. В зависимости от того, к какой шкале измерений относятся переменные, участвующие в анализе, SPSS предлагает различные дистанционные меры и меры подобия.
Переменные, относящиеся к интервальной шкале (метрические переменные)
Для переменных такого рода на выбор предлагается восемь различных мер расстояния и мер сходства, которые мы и рассмотрим далее. Примером расчета послужат два наблюдения из файла assess.sav (см. гл. 20.3), для которых расстояние и подобие должны быть рассчитаны с использованием переменных t3 и t4:
| t3 | t4 | |
| Отто P. | 5 | 4 |
| Эльке М. | 4 | 10 |
Евклидова дистанция (расстояние)
Евклидова дистанция между двумя точками х и у – это наименьшее расстояние между ними. В двух- или трехмерном случае – это прямая, соединяющая данные точки. Общей формулой для n-мерного случая (n переменных) является: 1.
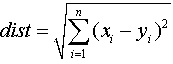
Сокращение dist, как и в следующей формуле, соответствует слову дистанция. Для приведенного примера получим:
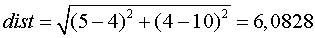
Квадрат евклидового расстояния
Этот вариант устанавливается по умолчанию. Благодаря возведению в квадрат при расчете лучше учитываются большие разности. Эта мера должна всегда использоваться при построении кластеров при помощи центроидного и медианного методов, а также метода Варда (Ward-Method) (см. разд. 20.5).
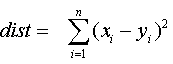
Для приведенного примера имеем:
cfot = (5 - 4) ^ 2 + (4 - 10) ^ 2 = 37Косинус
Как и для корреляционных коэффициентов Пирсона, область значений этой меры находится между -1 и +1.
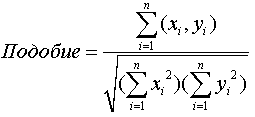
Для приведенного примера имеем: