Функции Бесселя-Кельвина. Сферические функции Бесселя.
Комплексная комбинация функций Бесселя-Кельвина вида ber(n,x) + i bei(n,x) является решением соответствующего ОДУ, зависящего от параметра n. Вид графиков функции bei для n=1 и 2 показан на рис. 10.6.
- bei (n,x) – мнимая часть функции Бесселя-Кельвина порядка n;
- ber(n,x) – действительная часть функции Бесселя-Кельвина порядка n;
- n – порядок (безразмерное неотрицательное целое число);
- х – действительный безразмерный скаляр.
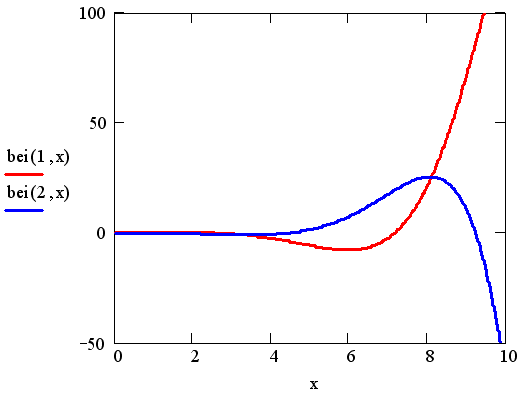
Рис. 10.6. Функции Бесселя-Кельвина
Сферические функции Бесселя
График сферических функций Бесселя первого порядка показан на рис. 10.7.
- js(n, z) – сферическая функция Бесселя первого рода порядка n, х>0;
- ys (n, z) – сферическая функция Бесселя второго рода порядка n, х>0;
- n – порядок (целое число), n>200;
- z – действительный или комплексный безразмерный скаляр, х>0.
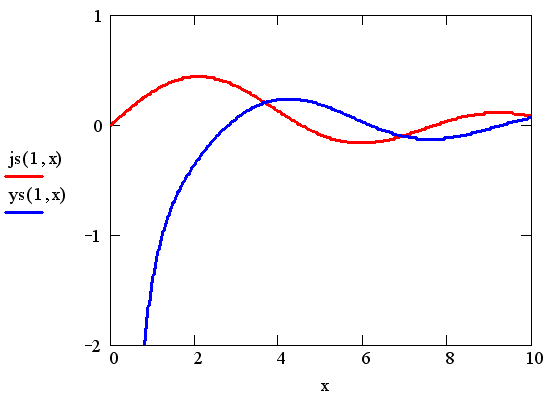
Рис. 10.7. Сферические функции Бесселя первого порядка
