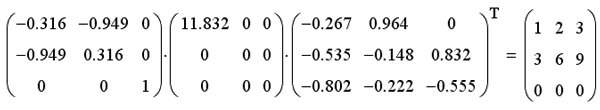Сингулярное разложение
Сингулярным разложением (singular value decomposition) матрицы А размера NXM (причем N>M) является разложение вида A=U S VT, где и и v – ортогональные матрицы размером NXN и мхм, соответственно, a s – диагональная матрица с сингулярными числами матрицы А на диагонали.
- svds (A) – вектор, состоящий из сингулярных чисел;
- svd (A) – сингулярное разложение;
- А – действительная матрица.
Примеры поиска сингулярных чисел невырожденной и сингулярной матрицы приведены в листингах 9.43 и 9.44, соответственно. Проверка правильности сингулярного разложения приведена в листинге 9.45. Вычисленные сингулярные числа находятся на главной диагонали средней матрицы (ее остальные элементы, по определению, равны нулю).
Сравнивая матрицы из листингов 9.44 и 9.45, Вы без труда разберетесь, каким образом следует выделять искомые матрицы сингулярного разложения из результата, поставляемого функцией svd.
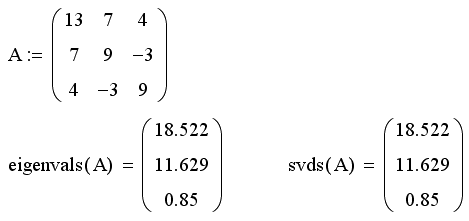
Листинг 9.43. Сингулярные числа и собственные значения невырожденной матрицы:
Листинг 9.44. Сингулярное разложение сингулярной матрицы:
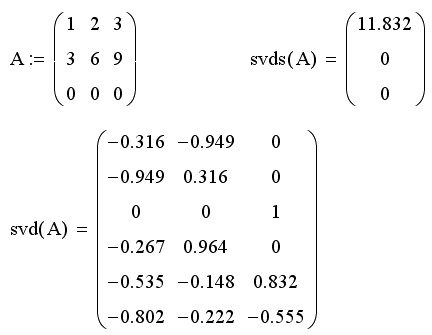
Листинг 9.45. Проверка сингулярного разложения (продолжение листинга 9.44):